题目内容
定义运算a*b=
,设函数f(x)=(2x+1)*(x+1),且关于x的方程f(x)=m恰有三个互不相等的实数根x1,x2,x3,则x1x2x3的取值范围是
|
(0,
)
| 9 |
| 4 |
(0,
)
.| 9 |
| 4 |
分析:先由新定义得出函数f(x)的解析式,进而画出其图象并求出方程f(x)=m取得三个根的条件,最后再求出x1x2x3的取值范围即可.
解答:解:由定义可知:f(x)=
,画出图象如图所示: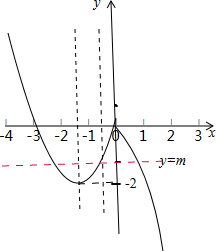
∵当x≤0时,f(x)=(x+
)2-2≥-2;当x>0时,f(x)=-(x+
)2+
<0.
∴当-2<m<0时,关于x的方程f(x)=m恰有三个互不相等的实数根x1,x2,x3,
不妨设x1<x2<x3,则x1,x2是方程x2+3x+
=m的两个根,x3是方程-x2-x=m的正根.
∴x1x2=
-m,x3=
.
∴x1x2x3=
(-2<m<0).
令
=t,即1-4m=t2.又∵-2<m<0,∴1<t<3.
φ(t)=
,
则φ′(t)=
=
,
∵1<t<3,∴φ′(t)>0,∴函数φ(t)在区间(1,3)上单调递增,∴φ(1)<φ(t)<φ(3),即0<φ(t)<
.
∴x1x2x3的取值范围是(0,
).
故答案为(0,
).
|
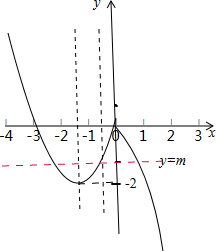
∵当x≤0时,f(x)=(x+
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
∴当-2<m<0时,关于x的方程f(x)=m恰有三个互不相等的实数根x1,x2,x3,
不妨设x1<x2<x3,则x1,x2是方程x2+3x+
| 1 |
| 4 |
∴x1x2=
| 1 |
| 4 |
| ||
| 2 |
∴x1x2x3=
(1-4m)(
| ||
| 8 |
令
| 1-4m |
φ(t)=
| t2(t-1) |
| 8 |
则φ′(t)=
| 3t2-2t |
| 8 |
3t(t-
| ||
| 8 |
∵1<t<3,∴φ′(t)>0,∴函数φ(t)在区间(1,3)上单调递增,∴φ(1)<φ(t)<φ(3),即0<φ(t)<
| 9 |
| 4 |
∴x1x2x3的取值范围是(0,
| 9 |
| 4 |
故答案为(0,
| 9 |
| 4 |
点评:本题考查的是新定义、方程的根的存在性及根的个数,由新定义正确得出函数的解析式并画出图象,进而求出方程f(x)=m取得三个根的条件是解题的关键.

练习册系列答案
相关题目