题目内容
对任意实数a、b,定义运算a*b=a2-ab-b2,则sin
*cos
=( )
| π |
| 12 |
| π |
| 12 |
分析:由新定义可得要求的式子等于 sin2
-sin
•cos
-cos2
,再利用二倍角公式求得结果.
| π |
| 12 |
| π |
| 12 |
| π |
| 12 |
| π |
| 12 |
解答:解:由题意可得sin
*cos
=sin2
-sin
•cos
-cos2
=-cos
-
sin
=-
-
=-
,
故选C.
| π |
| 12 |
| π |
| 12 |
| π |
| 12 |
| π |
| 12 |
| π |
| 12 |
| π |
| 12 |
=-cos
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
| ||
| 2 |
| 1 |
| 4 |
1+2
| ||
| 4 |
故选C.
点评:本题主要考查新定义,以及二倍角公式的应用,属于中档题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 ,2an+1=f(an)+15,bn=
,2an+1=f(an)+15,bn=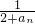 (n∈N*).
(n∈N*). )n]≤Sn<2.
)n]≤Sn<2. ,2an+1=f(an)+15,bn=
,2an+1=f(an)+15,bn=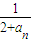 (n∈N*).已知不等式|f(x)≤2x2+4x-30|对任意实数x均成立.
(n∈N*).已知不等式|f(x)≤2x2+4x-30|对任意实数x均成立.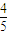 )n]≤Sn<2.
)n]≤Sn<2.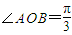 ,求曲线C的方程;
,求曲线C的方程;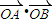 为定值T?指出T的值;
为定值T?指出T的值;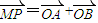 ,当a=-2,m变化时,求点P的轨迹方程;
,当a=-2,m变化时,求点P的轨迹方程;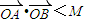 恒成立?如果存在,求出的M得最小值;如果不存在,说明理由.
恒成立?如果存在,求出的M得最小值;如果不存在,说明理由.