题目内容
A 任意a,b∈R,定义运算a*b=
,则f(x)=x*lnx的最大值为
B 对于函数①f(x)=4x+
-5;②f(x)=|log2x|-(
)x;③f(x)=cos(x+2)-cosx;
命题甲:f(x)在区间(1,2)上是增函数;
命题乙:f(x)在区间(0,+∞)上恰有两个零点x1,x2,且x1x2<1.
能使命题甲、乙均为真命题的函数序号是
|
0
0
B 对于函数①f(x)=4x+
| 1 |
| x |
| 1 |
| 2 |
命题甲:f(x)在区间(1,2)上是增函数;
命题乙:f(x)在区间(0,+∞)上恰有两个零点x1,x2,且x1x2<1.
能使命题甲、乙均为真命题的函数序号是
①②
①②
.分析:A:函数f(x)的取值与自变量x与1的大小有关,且其定义域为(0,+∞),所以分别讨论x>1和0<x≤1时函数的取值范围,即可比较得函数f(x)的最大值;
B:函数①可利用导数证明其在(1,2)上是增函数,利用函数在(0,+∞)上的单调性和极值,可证明f(x)在区间(0,+∞)上恰有两个零点x1,x2,且两零点均在区间(0,1)上,从而符合条件;函数②可利用对数函数和指数函数的单调性判断其在(1,2)上是增函数,再利用数形结合判断f(x)在区间(0,+∞)上恰有两个零点x1,x2,并利用指数函数的单调性证明x1x2<1.函数③显然不符合命题乙的要求
B:函数①可利用导数证明其在(1,2)上是增函数,利用函数在(0,+∞)上的单调性和极值,可证明f(x)在区间(0,+∞)上恰有两个零点x1,x2,且两零点均在区间(0,1)上,从而符合条件;函数②可利用对数函数和指数函数的单调性判断其在(1,2)上是增函数,再利用数形结合判断f(x)在区间(0,+∞)上恰有两个零点x1,x2,并利用指数函数的单调性证明x1x2<1.函数③显然不符合命题乙的要求
解答:解:A:当x>1时,lnx>0,f(x)=x*lnx=-
<0,
当0<x≤1时,lnx≤0,f(x)=x*lnx=xlnx≤0 (当且仅当x=1时取等号)
∴f(x)=x*lnx的最大值为0
故答案为 0
B:①f′(x)=4-
=
∴f(x)=4x+
-5在(0,
)上为减函数,在(
,+∞)上为增函数
而f(
)=2+2-5=-1<0,f(
)=
+8-5>0,f(1)=4+1-5=0,f(2)=8+
-5>0
∴函数f(x)在区间(0,+∞)上恰有两个零点x1,x2,且两根均在区间(0,1)上,
∴函数f(x)在区间(1,2)上是增函数且在区间(0,+∞)上恰有两个零点x1,x2,且x1x2<1.①符合题意
②∵当x∈(1,2)时,log2x>0,
∴f(x)=log2x-(
)x,y=log2x和y=-(
)x在(1,2)上均为增函数,
∴函数f(x)在区间(1,2)上是增函数,
画出函数y=|log2x|,和y=(
)x的图象如图:
可知f(x)在区间(0,+∞)上恰有两个零点x1,x2,且设x1<x2,
∴|log2x1|>|log2x2|,
∴-log2x1>log2x2,
即log2x1+log2x2<0,∴x1x2<1
∴函数f(x)在区间(0,+∞)上恰有两个零点x1,x2,且x1x2<1
②符合题意
③由于y=cos(x+2)与y=cosx在(0,+∞)上有无数个交点
f(x)=cos(x+2)-cosx在(0,+∞)上有无数个零点,
③不符合题意
故答案为①②
| x |
| lnx |
当0<x≤1时,lnx≤0,f(x)=x*lnx=xlnx≤0 (当且仅当x=1时取等号)
∴f(x)=x*lnx的最大值为0
故答案为 0
B:①f′(x)=4-
| 1 |
| x2 |
| (2x+1)(2x-1) |
| x2 |
∴f(x)=4x+
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
而f(
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
∴函数f(x)在区间(0,+∞)上恰有两个零点x1,x2,且两根均在区间(0,1)上,
∴函数f(x)在区间(1,2)上是增函数且在区间(0,+∞)上恰有两个零点x1,x2,且x1x2<1.①符合题意
②∵当x∈(1,2)时,log2x>0,
∴f(x)=log2x-(
| 1 |
| 2 |
| 1 |
| 2 |
∴函数f(x)在区间(1,2)上是增函数,
画出函数y=|log2x|,和y=(
| 1 |
| 2 |

可知f(x)在区间(0,+∞)上恰有两个零点x1,x2,且设x1<x2,
∴|log2x1|>|log2x2|,
∴-log2x1>log2x2,
即log2x1+log2x2<0,∴x1x2<1
∴函数f(x)在区间(0,+∞)上恰有两个零点x1,x2,且x1x2<1
②符合题意
③由于y=cos(x+2)与y=cosx在(0,+∞)上有无数个交点
f(x)=cos(x+2)-cosx在(0,+∞)上有无数个零点,
③不符合题意
故答案为①②
点评:本题综合考查了对新定义函数的理解和运用,分段函数求最值的方法,函数单调性的判断方法,函数零点个数的判断方法及其证明,有一定难度

练习册系列答案
相关题目
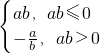 ,则f(x)=x*lnx的最大值为________
,则f(x)=x*lnx的最大值为________ -5;②f(x)=|log2x|-
-5;②f(x)=|log2x|-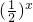 ;③f(x)=cos(x+2)-cosx;
;③f(x)=cos(x+2)-cosx; ,则f(x)=x*lnx的最大值为
,则f(x)=x*lnx的最大值为  -5;②f(x)=|log2x|-
-5;②f(x)=|log2x|- ;③f(x)=cos(x+2)-cosx;
;③f(x)=cos(x+2)-cosx;