题目内容
已知Rt△ABC中,∠ABC=90°,AB=4,BC=2,D,E分别是AB,AC的中点,将△ADE沿着DE翻折成△A1DE,使得平面A1DE⊥平面DECB,F是A1B上一点且A1E∥平面FDC.(1)求
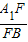 .
.(2)求三棱锥D-A1CF的体积.
(3)求A1B与平面FDC所成角的大小.
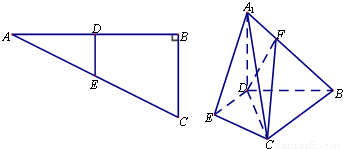
【答案】分析:(1)连接EB交DC于O,连接FO,由线面平行的性质定理可得A1E∥FO,由三角形中位定理及相似三角形的性质可得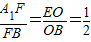
(2)由面面垂直的性质定理可得A1D⊥平面DECB,代入棱锥体积公式可得三棱锥D-A1CF的体积.
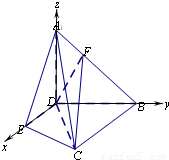
(3)以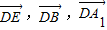 为正交基底建立如图所示的空间直角坐标系D-xyz.分别求出平面FDC的法向量和直线A1B的方向向量,代入向量坐标公式,可得答案.
为正交基底建立如图所示的空间直角坐标系D-xyz.分别求出平面FDC的法向量和直线A1B的方向向量,代入向量坐标公式,可得答案.
解答: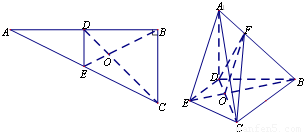 解:(1)连接EB交DC于O,连接FO.
解:(1)连接EB交DC于O,连接FO.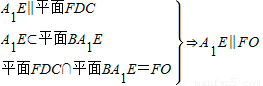 .…(3分)
.…(3分)
D,E分别是AB,AC的中点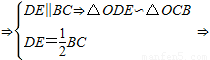
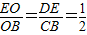 .
.
所以在△BA1E中,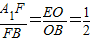 .…(5分)
.…(5分)
(2) .
.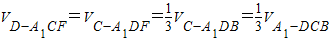 =
= .…(10分)
.…(10分)
(3)A1D⊥平面DECB.又DE⊥DB.
以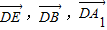 为正交基底建立如图所示的空间直角坐标系D-xyz.
为正交基底建立如图所示的空间直角坐标系D-xyz.
则D(0,0,0),A1(0,0,2),B(0,2,0),C(2,2,0).…(7分)
设F(x,y,z).因为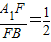 .
.
所以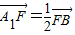 ,即
,即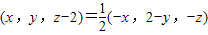 ,
,
所以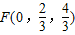 .
.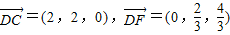 .设平面FDC的法向量
.设平面FDC的法向量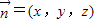 .
.
则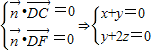 ,令z=1,则
,令z=1,则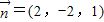 .又
.又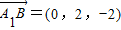 .
.
设A1B与平面FDC所成角的大小为θ,则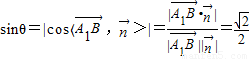 .
.
因为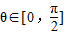 ,所以A1B与平面FDC所成角的大小
,所以A1B与平面FDC所成角的大小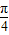 .…(15分)
.…(15分)
点评:本题考查的知识点是直线与平面所成的角,直线与平面平行的性质定理,三棱锥的体积,其中建立空间坐标系,将空间直线与平面的夹角转化为向量夹角是解答的关键.
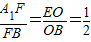
(2)由面面垂直的性质定理可得A1D⊥平面DECB,代入棱锥体积公式可得三棱锥D-A1CF的体积.
(3)以
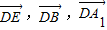 为正交基底建立如图所示的空间直角坐标系D-xyz.分别求出平面FDC的法向量和直线A1B的方向向量,代入向量坐标公式,可得答案.
为正交基底建立如图所示的空间直角坐标系D-xyz.分别求出平面FDC的法向量和直线A1B的方向向量,代入向量坐标公式,可得答案.解答:
 解:(1)连接EB交DC于O,连接FO.
解:(1)连接EB交DC于O,连接FO.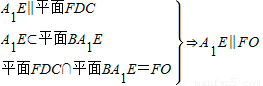 .…(3分)
.…(3分)D,E分别是AB,AC的中点
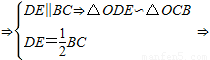
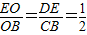 .
.所以在△BA1E中,
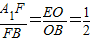 .…(5分)
.…(5分)(2)
 .
.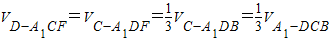 =
= .…(10分)
.…(10分)(3)A1D⊥平面DECB.又DE⊥DB.
以
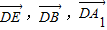 为正交基底建立如图所示的空间直角坐标系D-xyz.
为正交基底建立如图所示的空间直角坐标系D-xyz.则D(0,0,0),A1(0,0,2),B(0,2,0),C(2,2,0).…(7分)
设F(x,y,z).因为
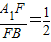 .
.
所以
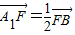 ,即
,即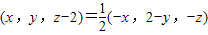 ,
,所以
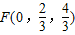 .
.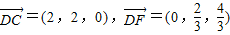 .设平面FDC的法向量
.设平面FDC的法向量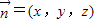 .
.则
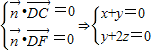 ,令z=1,则
,令z=1,则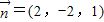 .又
.又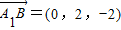 .
.设A1B与平面FDC所成角的大小为θ,则
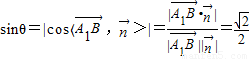 .
.因为
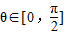 ,所以A1B与平面FDC所成角的大小
,所以A1B与平面FDC所成角的大小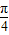 .…(15分)
.…(15分)点评:本题考查的知识点是直线与平面所成的角,直线与平面平行的性质定理,三棱锥的体积,其中建立空间坐标系,将空间直线与平面的夹角转化为向量夹角是解答的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
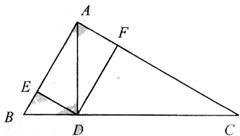 已知Rt△ABC中,∠BAC=90°,AD⊥BC,垂足为D,DF⊥AC,垂足为F,DE⊥AB,垂足为E.
已知Rt△ABC中,∠BAC=90°,AD⊥BC,垂足为D,DF⊥AC,垂足为F,DE⊥AB,垂足为E. 如图,已知Rt△ABC 中,AB=AC=
如图,已知Rt△ABC 中,AB=AC=
