题目内容
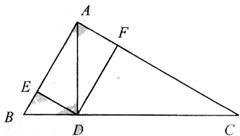已知Rt△ABC中，∠BAC=90°，AD⊥BC，垂足为D，DF⊥AC，垂足为F，DE⊥AB，垂足为E．求证：（Ⅰ）AB•AC=AD•BC；
（Ⅱ）AD3=BC•BE•CF
分析：对于（Ⅰ）求证AB•AC=AD•BC．故可考虑根据已知条件分析得到△ABD∽△CBA，根据相似三角形边成比例，即可得到答案．
对于（Ⅱ）求证AD3=BC•BE•CF．因为由射影定理可得到AD2=AE•AB，然后根据相似三角形证明DF=AE，及边的比例关系，综合三个条件即可得到答案．
对于（Ⅱ）求证AD3=BC•BE•CF．因为由射影定理可得到AD2=AE•AB，然后根据相似三角形证明DF=AE，及边的比例关系，综合三个条件即可得到答案．
解答：（Ⅰ）证明：因为Rt△ABC中，∠BAC=90°，AD⊥BC．
显然△ABD∽△CBA
∴
=
，即AB•AC=AD•BC
（Ⅱ）∵由射影定理知AD2=AE•AB
又由三角形相似可知
=
，
=
，且DF=AE
∴AE•AB•AD=BC•CF•BE，结合射影定理
∴AD3=BC•BE•CF．
故得证．
显然△ABD∽△CBA
∴
| AB |
| AD |
| BC |
| AC |
（Ⅱ）∵由射影定理知AD2=AE•AB
又由三角形相似可知
| DF |
| CF |
| BE |
| ED |
| AB |
| BC |
| ED |
| AD |
∴AE•AB•AD=BC•CF•BE，结合射影定理
∴AD3=BC•BE•CF．
故得证．
点评：此题主要考查相似三角形的性质问题，其中涉及到射影定理的应用．对于相似三角形在初中就已经学过，是大家比较熟悉的考点了，且题目较简单，属于基础题目．
练习册系列答案
阅读快车系列答案
相关题目
如图，已知Rt△ABC 中，AB=AC=
．
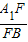