题目内容
 如图,已知Rt△ABC 中,AB=AC=
如图,已知Rt△ABC 中,AB=AC=| 2 |
(1)求证:平面ABD⊥平面BDC;
(2)求证:∠BAC=60°
(3)求点D到平面ABC的距离.
分析:(1)由原直角三角形中,AD是斜边BD上的高,得到AD与DB、DC都垂直,利用线面垂直的判定得到AD垂直于面BDC,由线面垂直的性质得到要证得结论;
(2)由原题给出的边的长度,通过解直角三角形分别求出三角形ABC三边的长度,然后利用余弦定理求解∠BAC的大小;
(3)取BC中点E,连结AE、DE后证明平面ADE和平面ABC垂直,在面ADE中作出D与平面ABC的垂线,在直角三角形ADE中,由等积法求得点D到平面ABC的距离.
(2)由原题给出的边的长度,通过解直角三角形分别求出三角形ABC三边的长度,然后利用余弦定理求解∠BAC的大小;
(3)取BC中点E,连结AE、DE后证明平面ADE和平面ABC垂直,在面ADE中作出D与平面ABC的垂线,在直角三角形ADE中,由等积法求得点D到平面ABC的距离.
解答: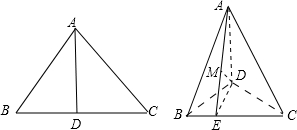 (1)证明:如图,
(1)证明:如图,
∵AD⊥BC,AD⊥DC,BD∩DC=D,∴AD⊥平面BDC.
又AD?平面ABD,∴平面ABD⊥平面BDC;
(2)证明:在原Rt△ABC中,AB=AC=
,∴BC=2,
∴BD=DC=1,又折叠后∠BDC=90°,
∴△BDC为等腰Rt△,∴BC=
,∴AB=BC=AC,∴∠BAC=60°;
(3)解:取BC的中点E,∵AB=AC,BD=DC,
∴DE⊥BC,AE⊥BC,∴BC⊥平面ADE,过D点作DM⊥AE,则DM⊥平面ABC.
在Rt△ADE中,AD=1,DE=
,∴AE=
,
∴斜边AE上的高DM=
=
=
.
∴D点到平面ABC的距离为
.
 (1)证明:如图,
(1)证明:如图,∵AD⊥BC,AD⊥DC,BD∩DC=D,∴AD⊥平面BDC.
又AD?平面ABD,∴平面ABD⊥平面BDC;
(2)证明:在原Rt△ABC中,AB=AC=
| 2 |
∴BD=DC=1,又折叠后∠BDC=90°,
∴△BDC为等腰Rt△,∴BC=
| 2 |
(3)解:取BC的中点E,∵AB=AC,BD=DC,
∴DE⊥BC,AE⊥BC,∴BC⊥平面ADE,过D点作DM⊥AE,则DM⊥平面ABC.
在Rt△ADE中,AD=1,DE=
| ||
| 2 |
| ||
| 2 |
∴斜边AE上的高DM=
| AD•DE |
| AE |
1×
| ||||
|
| ||
| 3 |
∴D点到平面ABC的距离为
| ||
| 3 |
点评:本题考查了平面与平面垂直的判定,考查了点线面间距离的计算,考查了学生的空间想象能力和思维能力,解答的关键是对折叠问题折叠前后的变量与不变量的掌握,是中档题.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 (A)(几何证明选讲选做题)如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径作圆与斜边AB交于点D,则BD的长为=
(A)(几何证明选讲选做题)如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径作圆与斜边AB交于点D,则BD的长为= (2013•汕头二模)如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC边为直径与AB交于点D,则三角形ACD的面积为
(2013•汕头二模)如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC边为直径与AB交于点D,则三角形ACD的面积为 (考生注意:请在二题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在二题中任选一题作答,如果多做,则按所做的第一题评分) (2012•湖南模拟)选做题(请考生在第16题的三个小题中任选两题作答,如果全做,则按前两题记分,要写出必要的推理与演算过程)
(2012•湖南模拟)选做题(请考生在第16题的三个小题中任选两题作答,如果全做,则按前两题记分,要写出必要的推理与演算过程)