题目内容
 直线l:y=k(x-1)过已知椭圆C:
直线l:y=k(x-1)过已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 1 |
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l交y轴于点M,且
| MA |
| AF |
| MB |
| BF |
(Ⅲ)连接AE、BD,试探索当直线l的倾斜角变化时,直线AE与BD是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由.
分析:(Ⅰ)由题设知b=
,e=
=
,因为a2=b2+c2a2=4,c2=1,由此能求出椭圆C的方程.
(Ⅱ)设直线l方程y=k(x-1),且l与y轴交于M(0,-1),设直线l交椭圆于A(x1,y1),B(x2,y2),由
得(3+4k2)x2-8k2x+4k2-12=0,再由韦达定理结合题设条件能够推导出当直线l的倾斜角变化时,λ+μ的值为定值-
.
(Ⅲ)当直线l斜率不存在时,直线l⊥X轴,则ABED为矩形,由对称性知,AE与BD相交FK的中点N(
,0),猜想,当直线l的倾斜角变化时,AE与BD相交于定点N(
,0).
证明:由A(x1,y1),B(x2,y2),知D(4,y1),E(4,y2).当直线l的倾斜角变化时,首先证直线AE过定点N(
,0),再证点N(
,0)也在直线lBD上;所以当m变化时,AE与BD相交于定点(
,0).
| 3 |
| c |
| a |
| 1 |
| 2 |
(Ⅱ)设直线l方程y=k(x-1),且l与y轴交于M(0,-1),设直线l交椭圆于A(x1,y1),B(x2,y2),由
|
| 8 |
| 3 |
(Ⅲ)当直线l斜率不存在时,直线l⊥X轴,则ABED为矩形,由对称性知,AE与BD相交FK的中点N(
| 5 |
| 2 |
| 5 |
| 2 |
证明:由A(x1,y1),B(x2,y2),知D(4,y1),E(4,y2).当直线l的倾斜角变化时,首先证直线AE过定点N(
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
解答:解:(Ⅰ)由题设知b=
,e=
=
,因为a2=b2+c2a2=4,c2=1,∴椭圆C的方程
+
=1(3分)
(Ⅱ)易知直线l的斜率存在,设直线l方程y=k(x-1),且l与y轴交于M(0,-k),设直线l交椭圆于A(x1,y1),B(x2,y2)
由
得(3+4k2)x2-8k2x+4k2-12=0,
∴x1+x2=
,x1•x2=
(6分)
又由
=λ
,
∴(x1,y1)=λ(1-x1,-y1),
∴λ=
,同理∴μ=
(8分)
∴λ+μ=
+
=
=-
所以当直线l的倾斜角变化时,λ+μ的值为定值-
;(10分)
(Ⅲ)当直线l斜率不存在时,直线l⊥X轴,则ABED为矩形,由对称性知,AE与BD相交FK的中点N(
,0),
猜想,当直线l的倾斜角变化时,AE与BD相交于定点N(
,0)(11分)
证明:由(Ⅱ)知A(x1,y1),B(x2,y2),∴D(4,y1),E(4,y2)
当直线l的倾斜角变化时,首先证直线AE过定点N(
,0),∵lAE:y-y2=
•(x-4)
当x=
时,y=y2+
•(-
)=
=
=
=
=0∴点N(
,0)在直线lAE上,同理可证,点N(
,0)也在直线lBD上;∴当m变化时,AE与BD相交于定点(
,0)
| 3 |
| c |
| a |
| 1 |
| 2 |
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)易知直线l的斜率存在,设直线l方程y=k(x-1),且l与y轴交于M(0,-k),设直线l交椭圆于A(x1,y1),B(x2,y2)
由
|
∴x1+x2=
| 8k2 |
| 3+4k2 |
| 4k2-12 |
| 3+4k2 |
又由
| MA |
| AF |
∴(x1,y1)=λ(1-x1,-y1),
∴λ=
| x1 |
| 1-x1 |
| x2 |
| 1-x2 |
∴λ+μ=
| x1 |
| 1-x1 |
| x2 |
| 1-x2 |
| x1+x2-2x1•x2 |
| 1-(x1+x2)+x1•x2 |
| 8 |
| 3 |
所以当直线l的倾斜角变化时,λ+μ的值为定值-
| 8 |
| 3 |
(Ⅲ)当直线l斜率不存在时,直线l⊥X轴,则ABED为矩形,由对称性知,AE与BD相交FK的中点N(
| 5 |
| 2 |
猜想,当直线l的倾斜角变化时,AE与BD相交于定点N(
| 5 |
| 2 |
证明:由(Ⅱ)知A(x1,y1),B(x2,y2),∴D(4,y1),E(4,y2)
当直线l的倾斜角变化时,首先证直线AE过定点N(
| 5 |
| 2 |
| y2-y1 |
| 4-x1 |
当x=
| 5 |
| 2 |
| y2-y1 |
| 4-x1 |
| 3 |
| 2 |
| 2(4-x1)•y2-3(y2-y1) |
| 2(4-x1) |
| 2(4-x1)•k(x2-1)-3k(x2-x1) |
| 2(4-x1) |
| 2(4-x1)•k(x2-1)-3k(x2-x1) |
| 2(4-x1) |
| -8k-2kx2x1+5k(x2+x1) |
| 2(4-x1) |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要灵活运用圆锥曲线性质,注意合理地进行等价转化.

练习册系列答案
相关题目
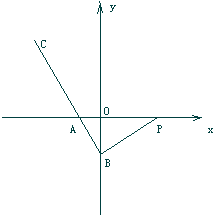 如图,已知直角三角形PAB的直角顶点为B,点P的坐标为(3,0),点B在y轴上,点A在x轴的负半轴上,在BA的延长线上取一点C,使
如图,已知直角三角形PAB的直角顶点为B,点P的坐标为(3,0),点B在y轴上,点A在x轴的负半轴上,在BA的延长线上取一点C,使