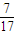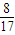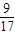题目内容
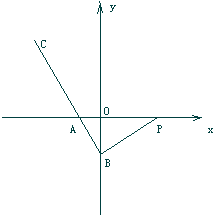 如图,已知直角三角形PAB的直角顶点为B,点P的坐标为(3,0),点B在y轴上,点A在x轴的负半轴上,在BA的延长线上取一点C,使
如图,已知直角三角形PAB的直角顶点为B,点P的坐标为(3,0),点B在y轴上,点A在x轴的负半轴上,在BA的延长线上取一点C,使| BC |
| BA |
(1)当B在y轴上移动时,求动点C的轨迹方程;
(2)若直线l:y=k(x-1)与点C的轨迹交于M、N两点,设D(-1,0),当∠MDN为锐角时,求的取值范围.
分析:(1)设C(x,y),A(a,0),B(0,b),其中a<0,b≠0.利用
=3
,可得(x,y-b)=3(a,-b),即x=3a,y=-2b.由于∠PBA=90°?
•
=0,可得b2=-3a.联立
,消去a,b即可.
(2)设M(x1,y1),N(x2,y2).联立
可得k2≠0,△>0,解得k的取值范围.可得根与系数的关系.由于∠MDN为锐角,可得
•
>0,代入即可.
| BC |
| BA |
| BP |
| BA |
|
(2)设M(x1,y1),N(x2,y2).联立
|
| DM |
| DN |
解答:解:(1)设C(x,y),A(a,0),B(0,b),其中a<0,b≠0.
∵
=3
,∴(x,y-b)=3(a,-b),∴x=3a,y=-2b.
∵∠PBA=90°,∴
•
=0,∴(3,-b)•(a,-b)=0,得b2=-3a.
联立
,消去a,b得到y2=-4x(x<0).
(2)设M(x1,y1),N(x2,y2).联立
化为k2x2-(2k2-4)x+k2=0,
∵k2≠0,△>0,解得0<k2<1.
∴x1+x2=
,x1x2=1.
∵∠MDN为锐角,∴
•
>0,∴(x1+1,y1)•(x2+1,y2)>0,化为x1x2+x1+x2+1+y1y2>0,
即x1x2+x1+x2+k2(x1-1)(x2-1)>0,整理为(1-k2)(x1+x2)+(1+k2)x1x2+1+k2>0,
代入解得k2>
,又0<k2<1.
联立得
<k2<1,解得k的取值范围是(-1,-
)∪(
,1).
∵
| BC |
| BA |
∵∠PBA=90°,∴
| BP |
| BA |
联立
|
(2)设M(x1,y1),N(x2,y2).联立
|
∵k2≠0,△>0,解得0<k2<1.
∴x1+x2=
| 2k2-4 |
| k2 |
∵∠MDN为锐角,∴
| DM |
| DN |
即x1x2+x1+x2+k2(x1-1)(x2-1)>0,整理为(1-k2)(x1+x2)+(1+k2)x1x2+1+k2>0,
代入解得k2>
| 1 |
| 2 |
联立得
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
点评:熟练掌握抛物线的标准方程与性质、直线与抛物线相交问题转化为方程联立得到△>0及根与系数的关系、向量垂直与数量积的关系、向量夹角与数量积的关系等是解题的关键.

练习册系列答案
相关题目
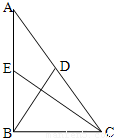
 (2012•武昌区模拟)如图,已知直角三角形△ABC的三边CB,BA,AC的长度成等差数列,点E为直角边AB的中点,点D在斜边AC上,且
(2012•武昌区模拟)如图,已知直角三角形△ABC的三边CB,BA,AC的长度成等差数列,点E为直角边AB的中点,点D在斜边AC上,且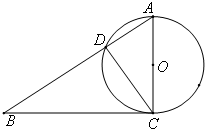 (2012•惠州一模)(几何证明选讲选做题)如图,已知直角三角形ABC中,∠ACB=90°,BC=4,AC=3,以AC为直径作圆O交AB于D,则CD=
(2012•惠州一模)(几何证明选讲选做题)如图,已知直角三角形ABC中,∠ACB=90°,BC=4,AC=3,以AC为直径作圆O交AB于D,则CD= 的三边
的三边 的长度成等差数列,点
的长度成等差数列,点 为直角边AB的中点,点D在斜边AC上,且
为直角边AB的中点,点D在斜边AC上,且 ,若
,若 ,则
,则

 B.
B.
 C.
C.
 D.
D.

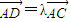 ,若CE⊥BD,则λ=( )
,若CE⊥BD,则λ=( )