题目内容
直线l:y=k(x-2)+2与圆x2+y2-2x-2y=0有两个不同的公共点,则k的取值范围是( )
分析:先将圆的方程化为标准方程,直线方程,化为一般方程.要使直线l:y=k(x-2)+2与圆x2+y2-2x-2y=0有两个不同的公共点,则圆心到直线的距离小于半径,故可求k的取值范围.
解答:解:将圆化为标准方程:(x-1)2+(y-1)2=2,直线l:y=k(x-2)+2可化为:kx-y-2k+2=0
要使直线l:y=k(x-2)+2与圆x2+y2-2x-2y=0有两个不同的公共点,则圆心到直线的距离小于半径
∴
<
∴k2+2k+1>0
∴k≠-1
∴k的取值范围是(-∞,-1)∪(-1,+∞)
故选D.
要使直线l:y=k(x-2)+2与圆x2+y2-2x-2y=0有两个不同的公共点,则圆心到直线的距离小于半径
∴
| |k-1-2k+2| | ||
|
| 2 |
∴k2+2k+1>0
∴k≠-1
∴k的取值范围是(-∞,-1)∪(-1,+∞)
故选D.
点评:本题以圆的方程为载体,考查直线与圆的位置关系,将直线l:y=k(x-2)+2与圆x2+y2-2x-2y=0有两个不同的公共点,转化为圆心到直线的距离小于半径是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
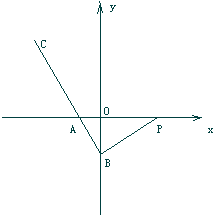 如图,已知直角三角形PAB的直角顶点为B,点P的坐标为(3,0),点B在y轴上,点A在x轴的负半轴上,在BA的延长线上取一点C,使
如图,已知直角三角形PAB的直角顶点为B,点P的坐标为(3,0),点B在y轴上,点A在x轴的负半轴上,在BA的延长线上取一点C,使