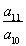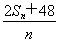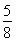Question

设等差数列{an}的前n项和为Sn，且S4＝－62，S6＝－75，求：

(1){an}的通项公式an及其前n项和Sn；

(2)|a1|＋|a2|＋|a3|＋…＋|a14|.

 

Answer 1

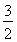（1）n2－n（2）147

【解析】(1)设等差数列首项为a1，公差为d，依题意得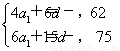解得a1＝－20，d＝3.

an＝a1＋(n－1)d＝3n－23，Sn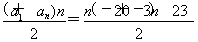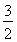＝＝n2－n.

(2)∵a1＝－20，d＝3，

∴{an}的项随着n的增大而增大．

设ak≤0且ak＋1≥0得3k－23≤0，且3(k＋1)－23≥0，

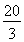∴≤k≤(k∈Z)，故k＝7.

即当n≤7时，an<0；当n≥8时，an>0.

∴|a1|＋|a2|＋|a3|＋…＋|a14|＝－(a1＋a2＋…＋a7)＋(a8＋a9＋…＋a14)＝S14－2S7＝147.