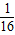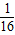Question

一动圆圆心在抛物线x²=-8y上，且动圆恒与直线y-2=0相切，则动圆必过定点（　　）

A．（4，0）

B．（0，-2）

C．（2，0）

D．（0，-4）

Answer 1

分析：首先由抛物线的方程可得直线y-2=0即为抛物线的准线方程，再结合抛物线的定义得到动圆一定过抛物线的焦点，进而得到答案．

解答：解：∵动圆圆心在抛物线x²=-8y上，且动圆恒与直线y-2=0相切，而抛物线的焦点为（0，-2），准线是y-2=0，
故动圆圆心到焦点的距离等于它到准线的距离，故动圆必过抛物线的焦点（0，-2），
故选B．

点评：本题主要考查抛物线的定义、标准方程，以及简单性质的应用，解决此类问题的关键是熟练掌握抛物线的定义，以及抛物线的有关性质与圆的定义，属于中档题．