题目内容
设△ABC的内角A,B,C所对的边分别为a,b,c.若三边的长为连续的三个正整数,且A>B>C,3b=20acosA,则sinA∶sinB∶sinC为( )
| A.4∶3∶2 |
| B.5∶6∶7 |
| C.5∶4∶3 |
| D.6∶5∶4 |
D
因为a,b,c为连续的三个正整数,且A>B>C,可得
a=c+2,b=c+1 ①
又因为3b=20acosA,由余弦定理可知cosA=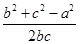 ,则
,则
3b=20a·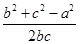 ②
②
联立①②,化简可得7c2-13c-60=0,解得c=4或c=-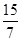 (舍去),则a=6,b=5.
(舍去),则a=6,b=5.
又由正弦定理可得,sinA∶sinB∶sinC=a∶b∶c=6∶5∶4.故选D.
a=c+2,b=c+1 ①
又因为3b=20acosA,由余弦定理可知cosA=
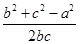 ,则
,则3b=20a·
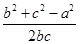 ②
②联立①②,化简可得7c2-13c-60=0,解得c=4或c=-
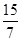 (舍去),则a=6,b=5.
(舍去),则a=6,b=5.又由正弦定理可得,sinA∶sinB∶sinC=a∶b∶c=6∶5∶4.故选D.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
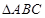 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为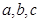 ,已知向量
,已知向量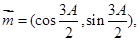
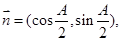 且满足
且满足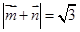 ,(1)求角A的大小;
,(1)求角A的大小;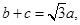 试判断
试判断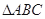 中,
中,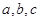 分别是角
分别是角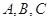 的对边,且
的对边,且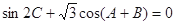 .
.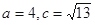 ,求
,求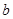 的长;
的长;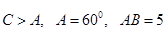 ,求
,求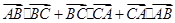 的值.
的值.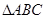 中,角
中,角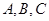 的对边分别为
的对边分别为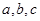 ,设S为△ABC的面积,满足4S=
,设S为△ABC的面积,满足4S=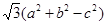 .
.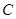 的大小;(2)若
的大小;(2)若 且
且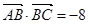 求
求 的值.
的值.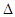 ABC中,已知sinA:sinB:sinC=3:5:7,则此三角形最大内角度数为为
ABC中,已知sinA:sinB:sinC=3:5:7,则此三角形最大内角度数为为 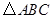 的面积
的面积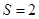 ,且
,且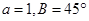 ,则
,则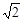
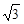
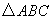 的三个内角A,B,C所对的边分别为
的三个内角A,B,C所对的边分别为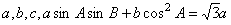 ,则
,则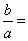 ( )
( )