题目内容
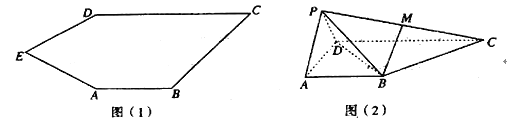
【题目】如图(1),五边形![]() 中,
中, ![]() .如图(2),将
.如图(2),将![]() 沿
沿![]() 折到
折到![]() 的位置,得到四棱锥
的位置,得到四棱锥![]() .点
.点![]() 为线段
为线段![]() 的中点,且
的中点,且![]() 平面
平面![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若直线![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]() ,设
,设![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:
(1)要证明面面垂直,一般先证线面垂直,题中已知![]() 平面
平面![]() ,由于
,由于![]() 是
是![]() 的中点,只要取
的中点,只要取![]() 的中点
的中点![]() ,可证
,可证![]() ,从而得
,从而得![]() 平面
平面![]() ,因此就得到面面垂直;
,因此就得到面面垂直;
(2)由(1)的垂直可证![]() 是等边三角形,因此有
是等边三角形,因此有![]() ,再得
,再得![]() ,于是有
,于是有![]() 平面
平面![]() ,可得
,可得![]() ,这样可求得图形中各线段长,可得四棱锥的底面积和高,得体积.
,这样可求得图形中各线段长,可得四棱锥的底面积和高,得体积.
试题解析:
(1)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() ,
,
又![]() ,所以
,所以![]() ,
,
则四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,
,
又![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
![]()
∴平面![]() 平面PCD;
平面PCD;
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
因为![]() 平面
平面![]() ,
,
∴![]() .
.
由![]() 即
即![]() 及
及![]() 为
为![]() 的中点,可得
的中点,可得![]() 为等边三角形,
为等边三角形,
∴![]() ,
,
又![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() 平面
平面![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
![]()
![]()
所以![]()
所以![]() .
.
![]() ,∴
,∴![]() 为直线
为直线![]() 与
与![]() 所成的角,
所成的角,
由(1)可得![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
由![]() ,可知
,可知![]() ,
,
则![]() .
.
其他方法酌情给分

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
【题目】甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 | 82 | 81 | 79 | 78 | 95 | 88 | 93 | 84 |
乙 | 92 | 95 | 80 | 75 | 83 | 80 | 90 | 85 |
(1)用茎叶图表示这两组数据;
(2)现要从中选派一人参加数学竞赛,从统计学的角度(在平均数、方差或标准差中选两个)考虑,你认为选派哪位学生参加合适?请说明理由.