题目内容
【题目】已知点A（3，3）、B（5，2）到直线l的距离相等，且直线l经过两直线l1：3x﹣y﹣1=0和l2：x+y﹣3=0的交点，求直线l的方程．
【答案】解：解方程组 
得交点P（1，2）． （i）若A、B在直线L的同侧，则L∥AB，
KAB= 
=﹣ 
，
∴直线的方程是：y﹣2=﹣ （x﹣1），
即x+2y﹣5=0．
（ii）若A、B分别在直线L的异侧，则直线L过线段AB的中点（4， 
），
∴直线L的两点式方程是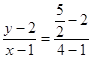 
，
即x﹣6y+11=0．
综（i）（ii）知直线L的方程是x+2y﹣5=0或x﹣6y+11=0
【解析】根据A、B在直线的同侧与异侧两种情况求解，在同侧时，利用直线平行则斜率相等求直线的斜率，从而求出直线方程；在异侧时，判定直线过线段的中点，利用两点式求直线方程．
【考点精析】掌握点斜式方程和两点式方程是解答本题的根本，需要知道直线的点斜式方程：直线
经过点
，且斜率为
则：
；直线的两点式方程：已知两点
其中
则：y-y1/y-y2=x-x1/x-x2．
练习册系列答案
寒假学与练系列答案
相关题目
