Question

如图所示，四棱锥P－ABCD的底面ABCD为一直角梯形，其中BA⊥AD，CD⊥AD，CD＝AD＝2AB，PA⊥底面ABCD，E是PC的中点．

(1)求证：BE∥平面PAD；

(2)若BE⊥平面PCD，求平面EBD与平面BDC夹角的余弦值．

 

Answer 1

（1）见解析（2）

【解析】设AB＝a，PA＝b，如图所示，建立空间直角坐标系，则A(0，0，0)，B(a，0，0)，P(0，0，b)，C(2a，2a，0)，D(0，2a，0)，E .

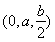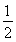
(1)证明：＝，＝(0，2a，0)，＝(0，0，b)，所以＝＋，又BE?平面PAD，AD?平面PAD，AP?平面PAD，故BE∥平面PAD.

(2)∵BE⊥平面PCD，∴BE⊥PC，即·＝0，

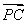＝(2a，2a，－b)，∴·＝2a2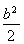－＝0，即b＝2a.

在平面BDE和平面BDC中，＝(0，a，a)，＝(－a，2a，0)，＝(a，2a，0)，

所以平面BDE的一个法向量为n1＝(2，1，－1)，平面BDC的一个法向量为n2＝(0，0，1)．

cos〈n1，n2〉＝－，所以平面EBD与平面BDC夹角的余弦值为.