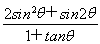题目内容
某旅游景点有一处山峰，游客需从景点入口A处向下沿坡角为α的一条小路行进a百米后到达山脚B处，然后沿坡角为β的山路向上行进b百米后到达山腰C处，这时回头望向景点入口A处俯角为θ，由于山势变陡到达山峰D坡角为γ，然后继续向上行进c百米终于到达山峰D处，游览风景后，此游客打算乘坐由山峰D直达入口A的缆车下山结束行程，如图所示，假设A，B，C，D四个点在同一竖直平面．
(1)求B，D两点的海拔落差h；
(2)求AD的长
（1）bsin β＋csin γ（2）
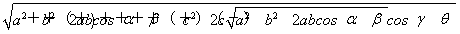
【解析】(1)h＝bsin β＋csin γ.
(2)方法一：联结AC.在△ABC中，由余弦定理得AC2＝a2＋b2＋2abcos(α＋β)，
在△ACD中，由余弦定理得AD2＝AC2＋c2－2cACcos(π－γ＋θ)，
所以AD＝.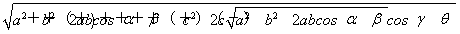
方法二：联结AC.在△ABC中，由正弦定理得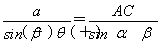
，所以AC＝
，
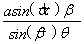以下同方法一．
练习册系列答案
相关题目
