题目内容
【题目】在△ABC中，∠A=60°，AB=3，AC=2．若 
=2 
， 
=λ 
﹣ 
（λ∈R），且 
=﹣4，则λ的值为 ．
【答案】
【解析】解：如图所示，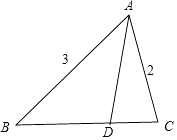
△ABC中，∠A=60°，AB=3，AC=2，
=2 
，
∴ 
= 
+
= + 
= + 
（ 
﹣ ）
= 
+ 
，
又 
=λ ﹣ （λ∈R），
∴ 
=（ + ）（λ ﹣ ）
=（ 
λ﹣ ） ﹣ 
+ λ 
=（ λ﹣ ）×3×2×cos60°﹣ ×32+ λ×22=﹣4，
∴ 
λ=1，
解得λ= ．
所以答案是： ．
【考点精析】利用向量的减法及其几何意义对题目进行判断即可得到答案，需要熟知向量减法的三角形法则：共起点，箭头指向被减向量．
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案【题目】微信红包是一款年轻人非常喜欢的手机应用.某网络运营商对甲、乙两个品牌各
种型号的手机在相同环境下抢到红包的个数进行统计，得到如下数据：
品牌 型号 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ |
甲品牌（个） | 4 | 3 | 8 | 6 | 12 |
乙品牌（个） | 5 | 7 | 9 | 4 | 3 |
红包个数 手机品牌 | 优良 | 一般 | 合计 |
甲品牌（个） | |||
乙品牌（个） | |||
合计 |
（Ⅰ）如果抢到红包个数超过个的手机型号为“优良”，否则为“一般”，请完成上述表格，并据此判断是否有
的把握认为抢到红包的个数与手机品牌有关？
（Ⅱ）不考虑其它因素，现要从甲、乙两品牌的种型号中各选出
种型号的手机进行促销活动，求恰有一种型号是“优良”，另一种型号是“一般”的概率；
参考公式：随机变量
的观察值计算公式：
，
其中
.临界值表：
| 0.10 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
【题目】某届奥运会上，中国队以26金18银26铜的成绩称金牌榜第三、奖牌榜第二，某校体育爱好者在高三年级一班至六班进行了“本届奥运会中国队表现”的满意度调查
结果只有“满意”和“不满意”两种
，从被调查的学生中随机抽取了50人，具体的调查结果如表：
班号 | 一班 | 二班 | 三班 | 四班 | 五班 | 六班 |
频数 | 5 | 9 | 11 | 9 | 7 | 9 |
满意人数 | 4 | 7 | 8 | 5 | 6 | 6 |
（1）在高三年级全体学生中随机抽取一名学生，由以上统计数据估计该生持满意态度的概率；
（2）若从一班至二班的调查对象中随机选取4人进行追踪调查，记选中的4人中对“本届奥运会中国队表现”不满意的人数为
，求随机变量的分布列及数学期望．
