题目内容
【题目】在平面直角坐标系中，以原点为极点，x轴正半轴为极轴建立极坐标系，并在两坐标系中取相同的长度单位.已知曲线C的极坐标方程为
，直线l的参数方程为
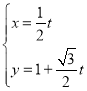，（t为参数）.
（1）求直线l的普通方程和曲线C的直角坐标方程；
（2）若直线l与曲线C交于A，B两点，
，且
，求
值.
【答案】（1）
，
；（2）
.
【解析】
（1）相切参数方程中的
，即可得到直线
的普通方程和，利用
，
代入
，即可化简曲线
的极坐标方程为直角坐标方程；
（2）利用直线参数方程的几何意义，结合韦达定理，化简求解
的值．
（1）由直线l的参数方程消去参数t，得直线l的普通方程为，
将，代入得，
曲线C的直角坐标方程为.
（2）设A，B对应的参数为
，
，
将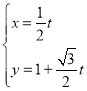
代入，得
，
所以
，
.
故直线l过
，且
，所以
，
.
于是
，
.
故
.
练习册系列答案
小夫子全能检测系列答案
相关题目
【题目】《中华人民共和国个人所得税》规定，公民全月工资、薪金所得不超过3500元的部分不必纳税，超过3500元的部分为全月应纳税所得额.此项税款按下表分段累计计算：
全月应纳税所得额 | 税率（ |
不超过1500元的部分 | 3 |
超过1500元至不超过4500元的部分 | 10 |
超过4500元至不超过9000元的部分 | 20 |
（1）试建立当月纳税款与当月工资、薪金（总计不超过12500元）所得的函数关系式；
（2）已知我市某国有企业一负责人十月份应缴纳税款为295元，那么他当月的工资、薪金所得是多少元？
