题目内容
9.函数f(x)=ax+b的图象过点(0,-2)和(2,0),则f(4)=6.分析 函数f(x)=ax+b(a>0)的图象经过点,代入就可以求出a,b的值,即可得出函数的解析式从而求出f(4).
解答 解:已知函数f(x)=ax+b(a>0)的图象经过点过点(0,-2)和(2,0),
则$\left\{\begin{array}{l}{{a}^{0}+b=-2}\\{{a}^{2}+b=0}\end{array}\right.$,解得a=$\sqrt{3}$,b=-3
因此函数的解析式是:f(x)=$\sqrt{3}$x-3.
∴f(4)=$\sqrt{3}$4-3=6,
故答案为:6.
点评 本题主要考查了函数解析式与图象上的点的关系,满足解析式的点在函数图象上,函数图象上的点满足解析式.

练习册系列答案
相关题目
20.log483+4log482等于( )
| A. | 1 | B. | 2 | C. | 6 | D. | 48 |
1.设M=${∫}_{1}^{2}$log${\;}_{\frac{1}{2}}$xdx,N=${∫}_{1}^{2}$log${\;}_{\frac{1}{3}}$xdx,则( )
| A. | M>N | B. | M<N | C. | |M|<|N| | D. | |M|=|N| |
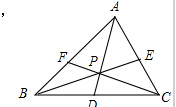 P为△ABC内一点,AP,BP,CP分别交对边于D,E,F.已知AP=BP=CP=6,设PD=x,PE=y,PF=z,xy+yz+zx=28,则xyz=24.
P为△ABC内一点,AP,BP,CP分别交对边于D,E,F.已知AP=BP=CP=6,设PD=x,PE=y,PF=z,xy+yz+zx=28,则xyz=24.