题目内容
已知函数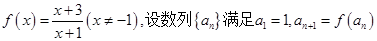 ,数列
,数列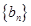 满足
满足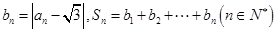
(1)用数学归纳法证明: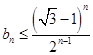 ;
;
(2)证明: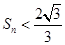
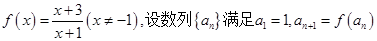 ,数列
,数列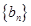 满足
满足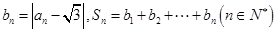
(1)用数学归纳法证明:
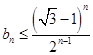 ;
;(2)证明:
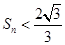
见解析
本试题主要考查了数列的运用。
解:(Ⅰ)证明:当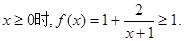 因为a1=1,所以
因为a1=1,所以
下面用数学归纳法证明不等式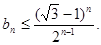
(1)当n=1时,b1=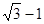 ,不等式成立,
,不等式成立,
(2)假设当n=k时,不等式成立,即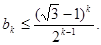 那么
那么 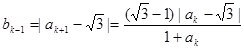
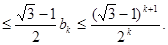
所以,当n=k+1时,不等也成立。
根据(1)和(2),可知不等式对任意n∈N*都成立。
(Ⅱ)证明:由(Ⅰ)知,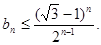
所以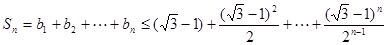
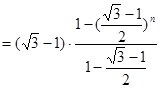
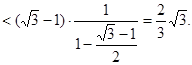
故对任意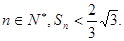
解:(Ⅰ)证明:当
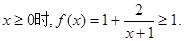 因为a1=1,所以
因为a1=1,所以
下面用数学归纳法证明不等式
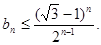
(1)当n=1时,b1=
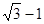 ,不等式成立,
,不等式成立,(2)假设当n=k时,不等式成立,即
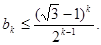 那么
那么 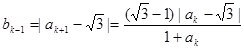
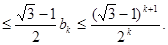
所以,当n=k+1时,不等也成立。
根据(1)和(2),可知不等式对任意n∈N*都成立。
(Ⅱ)证明:由(Ⅰ)知,
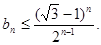
所以
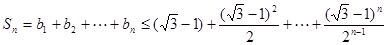
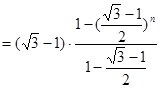
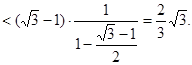
故对任意
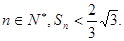

练习册系列答案
相关题目
 中,已知
中,已知 且
且
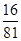 是这个等比数列中的项吗?如果是,指明是第几项;如果不是,请说明理由.
是这个等比数列中的项吗?如果是,指明是第几项;如果不是,请说明理由.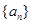 共有
共有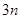 项,它的前
项,它的前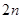 项的和为100,后
项的和为100,后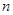 项的和等于 .
项的和等于 .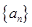 的公比
的公比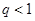 ,前
,前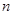 项和为
项和为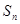 。已知
。已知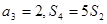 求
求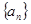 中,已知点
中,已知点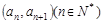 在函数
在函数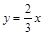 的图像上,且
的图像上,且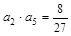 .
.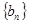 的前
的前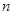 项和为
项和为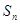 ,且
,且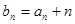 ,求
,求 为等差数列,且
为等差数列,且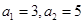 ,则
,则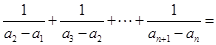 ( )
( )
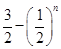
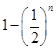
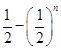
 中,
中, ,
, ,则
,则



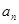 } 的各项都是正数,且
} 的各项都是正数,且 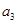
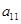 =16,则
=16,则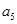 =( )
=( )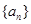 中,
中,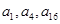 成等比数列,则
成等比数列,则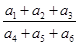 =
=