题目内容
在各项均为负数的数列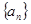 中,已知点
中,已知点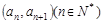 在函数
在函数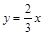 的图像上,且
的图像上,且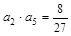 .
.
(Ⅰ)求证:数列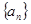 是等比数列,并求出其通项;
是等比数列,并求出其通项;
(Ⅱ)若数列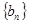 的前
的前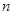 项和为
项和为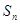 ,且
,且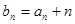 ,求
,求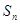 .
.
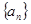 中,已知点
中,已知点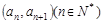 在函数
在函数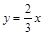 的图像上,且
的图像上,且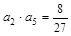 .
.(Ⅰ)求证:数列
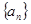 是等比数列,并求出其通项;
是等比数列,并求出其通项;(Ⅱ)若数列
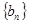 的前
的前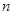 项和为
项和为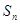 ,且
,且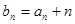 ,求
,求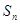 .
.(1)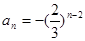 ;(2)
;(2)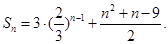 .
.
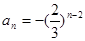 ;(2)
;(2)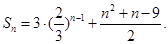 .
.本题考查等比数列的概念、通项,等比数列和等差数列的求和。高考对数列的考查难度在下降,其考查的重点转变为考查数列中的基本问题、两类基本数列,以及数列求和方面。解决两类基本数列问题的一个重要思想是基本量方法,即通过列出方程或者方程组求出等差数列的首项和公差、等比数列的首项和公比。数列求和要掌握好三个方法,一个是本题使用的分组求和,第二个是错位相减法,第三个是裂项求和法。(1)把点的坐标代入直线方程,根据等比数列的定义进行证明,显然公比是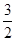 ,再根据条件
,再根据条件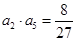 求出首项即可求出这个数列的通项公式;(2)数列
求出首项即可求出这个数列的通项公式;(2)数列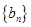 是一个等比数列和一个等差数列的对应项的和组成的数列,分别求和即可。
是一个等比数列和一个等差数列的对应项的和组成的数列,分别求和即可。
解:(1)因为点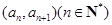 在函数
在函数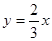 的图像上,所以
的图像上,所以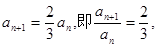 故数列
故数列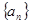 是公比
是公比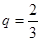 的等比数列因为
的等比数列因为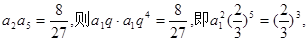 由于数列
由于数列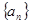 的各项均为负数,则
的各项均为负数,则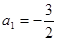 所以
所以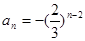 ………….6分
………….6分
(2)由(1)知,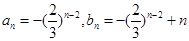 ,所以
,所以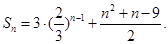 …12分
…12分
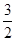 ,再根据条件
,再根据条件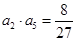 求出首项即可求出这个数列的通项公式;(2)数列
求出首项即可求出这个数列的通项公式;(2)数列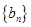 是一个等比数列和一个等差数列的对应项的和组成的数列,分别求和即可。
是一个等比数列和一个等差数列的对应项的和组成的数列,分别求和即可。解:(1)因为点
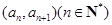 在函数
在函数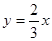 的图像上,所以
的图像上,所以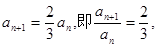 故数列
故数列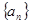 是公比
是公比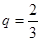 的等比数列因为
的等比数列因为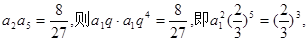 由于数列
由于数列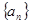 的各项均为负数,则
的各项均为负数,则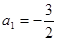 所以
所以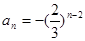 ………….6分
………….6分(2)由(1)知,
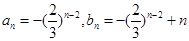 ,所以
,所以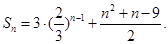 …12分
…12分
练习册系列答案
相关题目
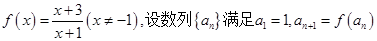 ,数列
,数列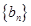 满足
满足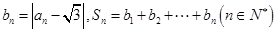
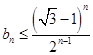 ;
;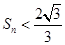
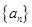 前n项和为
前n项和为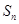 ,已知
,已知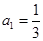 ,且对任意正整数m, n,都有
,且对任意正整数m, n,都有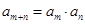 ,若
,若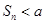 恒成立,则实数a的最小值为( )
恒成立,则实数a的最小值为( )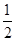
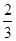
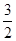
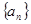 前
前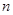 项的和为
项的和为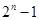 ,则数列
,则数列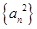 前
前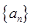 的前
的前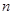 项和为
项和为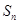 ,已知
,已知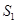 ,
,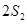 ,
,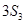 成等差数列,则
成等差数列,则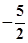
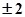
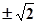
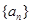 中,
中,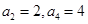 ,则
,则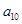 = ;
= ; 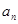 }中,已知
}中,已知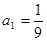 ,
,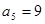 ,则
,则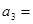 ( )
( )