题目内容
10.已知三棱锥的三视图如图所示,则它的外接球的体积为( )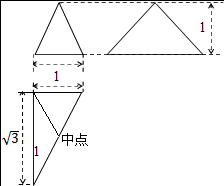
| A. | π | B. | 4π | C. | $\frac{2π}{3}$ | D. | $\frac{4π}{3}$ |
分析 由三视图可知该几何体是三棱锥,结合棱锥的几何特征,求出外接球的半径,代入球的体积公式,可得答案.
解答 解:由三视图可知该几何体是三棱锥,且三棱锥的高为1,底面为一个直角三角形,
由于底面斜边上的中线长为1,则底面的外接圆半径为1,
顶点在底面上的投影落在底面外接圆的圆心上,
由于顶点到底面的距离,与底面外接圆的半径相等则三棱锥的外接球半径R为1,
则三棱锥的外接球体积V=$\frac{4}{3}π×{1}^{3}$=$\frac{4π}{3}$,
故选:D
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
2.函数f(x)=x3+x-3的实数解落在的区间是( )
| A. | [0,1] | B. | [1,2] | C. | [2,3] | D. | [3,4] |
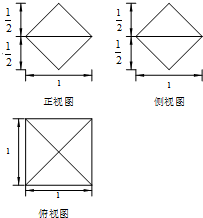 一个几何体的三视图如所示,则这个几何体的表面积为2$\sqrt{2}$.
一个几何体的三视图如所示,则这个几何体的表面积为2$\sqrt{2}$.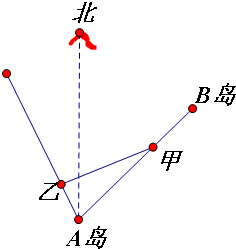 已知海岛B在海岛A的北偏东45°方向上,A、B相距10海里,小船甲从海岛B以2海里/小时的速度沿直线向海岛A移动,同时小船乙从海岛A出发沿北偏15°方向也以2海里/小时的速度移动
已知海岛B在海岛A的北偏东45°方向上,A、B相距10海里,小船甲从海岛B以2海里/小时的速度沿直线向海岛A移动,同时小船乙从海岛A出发沿北偏15°方向也以2海里/小时的速度移动