Question

【题目】已知圆与圆：关于直线对称，且点在圆上.

（1）判断圆与圆的位置关系；

（2）设为圆上任意一点，，，三点不共线，为的平分线，且交于. 求证：与的面积之比为定值.

Answer 1

【答案】（1）圆与圆相离；（2）定值为2.

【解析】试题分析：（1）若两圆关于直线对称，则圆心关于直线对称，并且两圆的半径相等，可先求得圆M的圆心，,然后根据圆心距与半径和比较大小，从而判断圆与圆的位置关系；（2）因为点G到AP和BP的距离相等，所以两个三角形的面积比值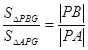,根据点P在圆M上，代入两点间距离公式求和,最后得到其比值.

试题解析：（1） ∵圆的圆心关于直线的对称点为，

∴，

∴圆的方程为.

∵，∴圆与圆相离.

（2） 设，则，

，

∴，∴.

∵为的角平分线上一点，∴到与的距离相等，

∴为定值.