题目内容
设二次函数f(x)=x2+bx+c(b,c∈R),已知不论α,β为何实数,恒有f(sinα)≥0,且f(2+cosβ)≤0.
(1)求证:b+c=-1;
(2)求c的取值范围;
(3)若函数f(sinα)的最大值为8,求b,c的值.
答案:
解析:
解析:
|
热点分析 (1)因为f(1)=1+b+c,所以本小题取特殊值α= (2)利用二次函数与一元二次不等式之间的关系,把f(2+cosβ)≤0恒成立条件转化为最值问题 (3)利用二次函数的单调性. 解答 (1)取α= 则f(1)≥0且f(1)≤0,∴f(1)=0,于是b+c=-1. (2)∵b=-1-c,∴f(x)=x2-(1+c)x+c=(x-1)(x-c). ∵1≤x≤3时,f(x)≤0,即(x-1)(x-c)≤0恒成立, ∴x-c≤0,即c≥x恒成立,∴c≥xmax=3. (3)f(sinα)=sin2α-(1+c)sinα+c=(sinα- ∵ 评析 本题充分体现了二次函数与二次不等式的联系与转化,其解法“巧”在利用条件的特殊状态求出f(1)=0,“活”在二次函数向不等式的转化,“妙”在利用二次函数单调性确定最大值的表达式,进而求出b,c. 综上可知,存在a=c= 采用取特值x=0,解代消元和判别式法,逐步确定待定参数. |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 R,且x+y+z=1,求证x2+y2+z2≥
R,且x+y+z=1,求证x2+y2+z2≥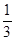 ;
; ,若x
,若x