题目内容
已知a,b为正实数.求证:
+
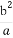≥a+b.
见解析
【解析】证明：方法一: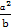
+
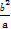-(a+b)
=
=
=
=
,
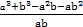
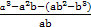
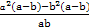
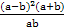又因为a>0,b>0,
所以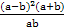≥0,
当且仅当a=b时等号成立.
所以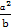+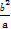≥a+b.
方法二:因为a>0,b>0,
所以(a+b)(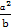+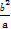)=a2+b2+
+
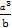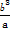≥a2+b2+2ab=(a+b)2.
所以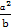+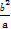≥a+b,
当且仅当a=b时等号成立.
练习册系列答案
相关题目
题目内容
已知a,b为正实数.求证:+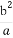≥a+b.
见解析
【解析】证明：方法一: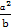+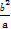-(a+b)
=
=
=
=,
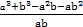
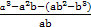
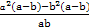
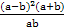又因为a>0,b>0,
所以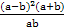≥0,
当且仅当a=b时等号成立.
所以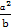+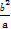≥a+b.
方法二:因为a>0,b>0,
所以(a+b)(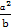+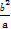)=a2+b2+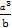+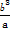≥a2+b2+2ab=(a+b)2.
所以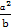+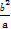≥a+b,
当且仅当a=b时等号成立.
