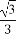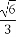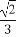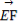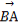Question

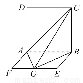
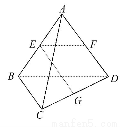
如图,已知正四棱锥P-ABCD的所有棱长都是2,底面正方形两条对角线相交于O点,M是侧棱PC的中点.

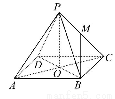
(1)求此正四棱锥的体积.

(2)求直线BM与侧面PAB所成角θ的正弦值.

 

Answer 1

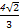(1) (2)

【解析】(1)由题可得,PO⊥底面ABCD.

在Rt△AOP中,

∵AO=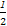AC=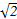,AP=2,

∴PO===.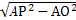

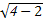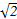故VP-ABCD=·S底·PO=×4×=.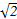

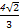(2)由(1)知PO⊥底面ABCD,且OA⊥OB,以O点为原点,OA,OB,OP所在的直线分别为x,y,z轴建立如图所示的空间直角坐标系,

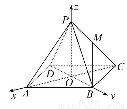
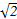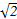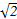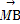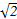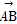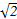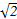则各点的坐标为A(,0,0),B(0,,0),P(0,0,),M(-,0,),

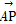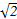∴=(,,-),=(-,,0),

=(-,0,).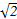

设平面ABP的一个法向量为n=(x,y,z),

则有即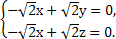

取x=1,则y=1,z=1,

∴n=(1,1,1),

∴sinθ=cos(90°-θ)===.