题目内容
已知等比数列{an}中,a2,a3,a4分别是某等差数列的第5项、第3项、第2项,且 ,公比q≠1.
,公比q≠1.
(1)求数列{an}的通项公式;
(2)已知数列{bn}满足:a1b1+a2b2+…+anbn=2n-1(n∈N*),求数列{bn}的前n项和Sn.
解:(1)由已知条件得a2-a3=2(a3-a4).
即a1(q-q2)=2a1(q2-q3)
整理得:2q3-3q2+q=0解得 或q=1(舍去)或q=0(舍去)
或q=1(舍去)或q=0(舍去)
所以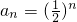 .
.
(2)当n=1时,a1b1=1,∴b1=2,
当n≥2时,a1b1+a2b2++an-1bn-1+anbn=2n-1(1)
a1b1+a2b2++an-1bn-1=2n-3(2)
(1)-(2)得:anbn=2
∵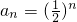 .∴bn=2n+1(n≥2)
.∴bn=2n+1(n≥2)
因此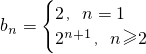
当n=1时,Sn=S1=b1=2;
当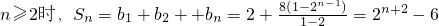 .
.
综上,Sn=2n+2-6.
分析:(1)求数列{an}的通项公式,{an}是等比数列,只要根据已知的条件求出首项和公比即可将通项公式写出来.
(2)则是根据数列an与bn的关系,求出数列bn的通项公式.然后用等比数列求和公式求出数列数列{bn}的前n项和Sn,注意s1单独求.
点评:本题是一个求数列通项和数列求和问题.求数列通项时,注意首项要单独求.求数列前n项和时,s1要单独球,学生容易犯错误.
即a1(q-q2)=2a1(q2-q3)
整理得:2q3-3q2+q=0解得
 或q=1(舍去)或q=0(舍去)
或q=1(舍去)或q=0(舍去)所以
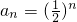 .
.(2)当n=1时,a1b1=1,∴b1=2,
当n≥2时,a1b1+a2b2++an-1bn-1+anbn=2n-1(1)
a1b1+a2b2++an-1bn-1=2n-3(2)
(1)-(2)得:anbn=2
∵
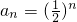 .∴bn=2n+1(n≥2)
.∴bn=2n+1(n≥2)因此
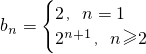
当n=1时,Sn=S1=b1=2;
当
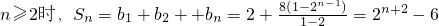 .
.综上,Sn=2n+2-6.
分析:(1)求数列{an}的通项公式,{an}是等比数列,只要根据已知的条件求出首项和公比即可将通项公式写出来.
(2)则是根据数列an与bn的关系,求出数列bn的通项公式.然后用等比数列求和公式求出数列数列{bn}的前n项和Sn,注意s1单独求.
点评:本题是一个求数列通项和数列求和问题.求数列通项时,注意首项要单独求.求数列前n项和时,s1要单独球,学生容易犯错误.

练习册系列答案
相关题目