题目内容
在R t △PAB中,PA=PB,点C、D分别在PA、PB上,且CD∥AB,AB=3,AC= ,则
,则 的值为( )
的值为( )
| A.-7 | B.0 | C.-3 | D.3 |
C
解析试题分析:建立如图所示的直角坐标系,
∵PA=PB,CD∥AB,AB=3,AC=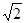
∴PA=PB=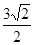 ,PC=
,PC=
∴A(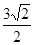 ,0),B(0,
,0),B(0,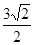 )C(
)C( ,0)D(0,
,0)D(0, )
)
∴ =(
=( ,
, ),
), =(
=( ,
, )
)
∴ =
=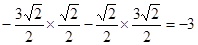
故选C
考点:平面向量数量积的运算.
点评:本题主要考查了向量的数量积的求解,解题的关键是建立坐标系,把所求问题坐标化.

练习册系列答案
相关题目
等边三角形ABC的边长为1, ,那么
,那么 等于( )
等于( )
A. | B. | C. | D.3 |
若非零向量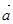 ,
, 满足
满足 ,且
,且 ,则向量
,则向量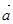 ,
, 的夹角为 ( )
的夹角为 ( )
A.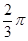 | B. | C. | D. |
已知向量 ,若
,若 则
则 的值为( )
的值为( )
A. | B. | C. | D. |
在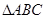 中,已知
中,已知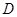 是
是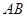 边上一点,若
边上一点,若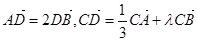 ,则
,则 等于
等于
A.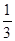 | B.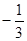 | C.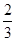 | D.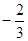 |
在直角坐标系 中,
中, 分别是与
分别是与 轴,
轴, 轴平行的单位向量,若直角三角形
轴平行的单位向量,若直角三角形 中,
中, ,
, ,则
,则 的可能值有( )
的可能值有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
已知不共线向量 则
则
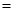
A. | B. | C. | D. |
若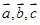 均为单位向量,且
均为单位向量,且 ,则
,则 的最大值为( )
的最大值为( )
| A.3 | B. | C.1 | D. +1 +1 |
已知
A. | B. | C. | D. |