题目内容
一个等比数列的首项为1，项数为偶数，其奇数项的和为85，偶数项的和为170，求项数n的值.解析：设该数列为{an}.由条件知
S偶=a2+a4+…+a2n=170，
S奇=a1+a3+…+a2n-1=85，
从而可知q=
=2.
∴85=a1+a3+…+a2n-1
=
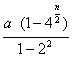=85,
即2n=256.
∴n=8.
练习册系列答案
导学教程高中新课标系列答案
相关题目
导学教程高中新课标系列答案题目内容
一个等比数列的首项为1，项数为偶数，其奇数项的和为85，偶数项的和为170，求项数n的值.解析：设该数列为{an}.由条件知
S偶=a2+a4+…+a2n=170，
S奇=a1+a3+…+a2n-1=85，
从而可知q==2.
∴85=a1+a3+…+a2n-1
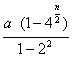==85,
即2n=256.
∴n=8.
导学教程高中新课标系列答案