题目内容
(1)若{an}是等差数列,首项a1>0,a2005+a2006>0,a2005•a2006<0,则使前n项和Sn>0成立的最大正整数n是(2)已知一个等比数列的首项为1,项数是偶数,其奇数项之和为85,偶数项和为170,则这个数列的公比等于
分析:(1)根据a2005•a2006<0判断出a2005和a2006异号,进而根据a2005+a2006>0,推断出a2005>0,a2006<0,进而利用等差数列求得公式以及等差中项的性质可知a1+a4010=a2005+a2006,根据a2005+a2006>0,判断出a1+a4010>0,进而求得n的值.
(2)先根据偶数项之和与奇数项之和的比为数列的公比,求得数列的公比,进而根据等比数列的求和公式,利用前n项的和求得项数n.
(2)先根据偶数项之和与奇数项之和的比为数列的公比,求得数列的公比,进而根据等比数列的求和公式,利用前n项的和求得项数n.
解答:解:(1)∵a2005•a2006<0,
∴a2005和a2006异号
∵a1>0,a2005+a2006>0,
∴a2005>0,a2006<0,
∵Sn=
>0
∴a1+an>0
∴a2005+a2006>0
∵a1+a4010=a2005+a2006,
∴a1+a4010>0
∴n最大为:4010
故答案为:4010
(2)∵q=
=
=2,
∴数列的前n项的和S=
=85+170=255
求得n=8
故答案为:2,8
∴a2005和a2006异号
∵a1>0,a2005+a2006>0,
∴a2005>0,a2006<0,
∵Sn=
| (a1 +an)×n |
| 2 |
∴a1+an>0
∴a2005+a2006>0
∵a1+a4010=a2005+a2006,
∴a1+a4010>0
∴n最大为:4010
故答案为:4010
(2)∵q=
| 偶数项之和 |
| 奇数项之和 |
| 170 |
| 85 |
∴数列的前n项的和S=
| (1-2n) |
| 1-2 |
求得n=8
故答案为:2,8
点评:本题主要考查了等比数列的性质,通项公式和前n项和的应用.考查了学生综合运用等比数列基础知识的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
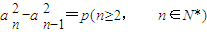 ( p为常数),则称{an}为“等方差数列”.下列是对“等方差数列”的判断:
( p为常数),则称{an}为“等方差数列”.下列是对“等方差数列”的判断: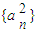 是等差数列;
是等差数列;