题目内容
已知矩阵A＝
，若点P(1，1)在矩阵A对应的变换作用下得到点P′(0，-8)．
(1)求实数a的值；
(2)求矩阵A的特征值．
，若点P(1，1)在矩阵A对应的变换作用下得到点P′(0，-8)．(1)求实数a的值；
(2)求矩阵A的特征值．
（1）a＝－9（2）－2或4
(1)由
＝
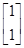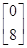，得a＋1＝－8，所以a＝－9.
(2)由(1)知A＝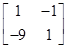
，则矩阵A的特征多项式为f(λ)＝
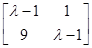＝(λ－1)2－9＝λ2－2λ－8，令f(λ)＝0，所以矩阵A的特征值为－2或4.
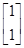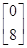＝，得a＋1＝－8，所以a＝－9.(2)由(1)知A＝
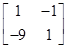，则矩阵A的特征多项式为f(λ)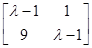＝＝(λ－1)2－9＝λ2－2λ－8，令f(λ)＝0，所以矩阵A的特征值为－2或4.
练习册系列答案
相关题目
及对应的一个特征向量
，并且矩阵M对应的变换将点
变换成
，求矩阵M。
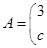
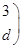，若矩阵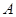
属于特征值6的一个特征向量为
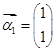，属于特征值1的一个特征向量
.
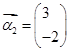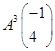
的变换
所对应的矩阵为
,将每个点横、纵坐标分别变为原来的
倍的变换
所对应的矩阵为
．
；
先在变换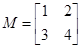
；
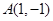在变换M作用下得到的点
；
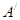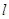在变换M作用下得到了直线
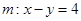，求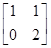
有特征向量为e1＝
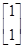，e2＝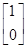
，
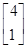，记作α＝e1＋3e2，利用这一表达式间接计算M4α，M10α.
，若矩阵M的逆矩阵M－1＝
，求a、b的值．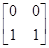
对应的变换作用下得到的图形．