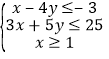题目内容
【题目】已知数列{an}的前n项和为Sn , 通项公式为 ![]() .
.
(Ⅰ)计算f(1),f(2),f(3)的值;
(Ⅱ)比较f(n)与1的大小,并用数学归纳法证明你的结论.
【答案】解:(Ⅰ)由已知 ![]() ,
, ![]() ,
, ![]() ;
;
(Ⅱ)由(Ⅰ)知f(1)>1,f(2)>1;当n≥3时,猜想:f(n)<1.
下面用数学归纳法证明:
①由(Ⅰ)当n=3时,f(n)<1;
②假设n=k(k≥3)时,f(n)<1,即 ![]() ,那么
,那么 ![]() =
= ![]()
![]() =
= ![]() =
= ![]() ,
,
所以当n=k+1时,f(n)<1也成立.由(1)和(2)知,当n≥3时,f(n)<1.
所以当n=1,和n=2时,f(n)>1;当n≥3时,f(n)<1
【解析】(1)此问根据通项公式计算出前n项的和.当n=1时,f(1)=s2;当n=2时,f(2)=s4﹣s1=a2+a3;当n=3时,f(3)=s6﹣s2 . (2)当n=1时, ![]() ≥1.当n≥2时,f(n)中没有a1 , 因此都小于1.
≥1.当n≥2时,f(n)中没有a1 , 因此都小于1.
【考点精析】认真审题,首先需要了解数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式).

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目