题目内容
设a,b,c为实数, .记集合S=
.记集合S= 若cardS,cardT分别为集合元素S,T的元素个数,则下列结论不可能的是( )
若cardS,cardT分别为集合元素S,T的元素个数,则下列结论不可能的是( )
(A)cardS=1, cardT=0 (B)cardS=1, cardT=1
(C)cardS=2, cardT=2 (D cardS="2," cardT=3
 .记集合S=
.记集合S= 若cardS,cardT分别为集合元素S,T的元素个数,则下列结论不可能的是( )
若cardS,cardT分别为集合元素S,T的元素个数,则下列结论不可能的是( )(A)cardS=1, cardT=0 (B)cardS=1, cardT=1
(C)cardS=2, cardT=2 (D cardS="2," cardT=3
D
分析:根据函数f(x)的解析可知f(x)=0时至少有一个根x=-a,然后讨论△=b2-4c可得根的个数,从而得到g(x)=0的根的个数,即可得到正确选项.
解答:解:∵f(x)=(x+a)(x2+bx+c),当f(x)=0时至少有一个根x=-a
当b2-4c=0时,f(x)=0还有一根 x=-
只要b≠-2a,f(x)=0就有2个根;当b=-2a,f(x)=0是一个根
当b2-4c<0时,f(x)=0只有一个根;
当b2-4c>0时,f(x)=0只有二个根或三个根
当a=b=c=0时cardS=1,cardT=0
当a>0,b=0,c>0时,cardS=1且cardT=1
当a=c=1,b=-2时,有cardS=2且cardT=2
故选D.
解答:解:∵f(x)=(x+a)(x2+bx+c),当f(x)=0时至少有一个根x=-a
当b2-4c=0时,f(x)=0还有一根 x=-

只要b≠-2a,f(x)=0就有2个根;当b=-2a,f(x)=0是一个根
当b2-4c<0时,f(x)=0只有一个根;
当b2-4c>0时,f(x)=0只有二个根或三个根
当a=b=c=0时cardS=1,cardT=0
当a>0,b=0,c>0时,cardS=1且cardT=1
当a=c=1,b=-2时,有cardS=2且cardT=2
故选D.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
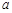 ,9)在函数
,9)在函数 的图像上,则tan
的图像上,则tan 的值为( )
的值为( )

 ,则
,则 的取值范围是( )
的取值范围是( ) )
) 是方程
是方程 的解,则
的解,则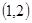



 ,函数
,函数 .
. 在[0,1]上的值域;
在[0,1]上的值域; [0,1],总存在
[0,1],总存在 [0,1],使得
[0,1],使得 成立,求
成立,求 的取值范围.
的取值范围.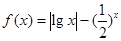 有两个零点
有两个零点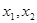 ,则有
,则有 





 ,则
,则 的值是
的值是 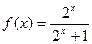 的值域为 .
的值域为 .