题目内容
设函数f(x)=sinx,g(x)=-9(
)2+9(
)-
,x∈(0,2π),则使g(x)≥f(x)的x的范围是( )
| x |
| π |
| x |
| π |
| 3 |
| 4 |
分析:当x∈(0,2π)时,利用验证排除法即可得答案.
解答:解:∵f(x)=sinx,g(x)=-9(
)2+9(
)-
,x∈(0,2π),
∴当x=0时,f(x)=0,g(0)=-
,f(x)>g(x),可排除A;
当x=
时,f(
)=sin
=-1,g(
)=-9×
+9×
-
=-7.5,f(x)>g(x),可排除B;
当x=
时,f(
)=
,g(
)=-9×
+9×
-
=
,满足g(x)≥f(x),可排除C,
故选D.
| x |
| π |
| x |
| π |
| 3 |
| 4 |
∴当x=0时,f(x)=0,g(0)=-
| 3 |
| 4 |
当x=
| 3π |
| 2 |
| 3π |
| 2 |
| 3π |
| 2 |
| 3π |
| 2 |
| 9 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
当x=
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 36 |
| 1 |
| 6 |
| 3 |
| 4 |
| 1 |
| 2 |
故选D.
点评:本题考查正弦函数的性质与二次函数的性质,着重考查验证排除法的应用,属于中档题.

练习册系列答案
相关题目
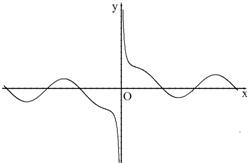 如图是函数Q(x)的图象的一部分,设函数f(x)=sinx,g ( x )=
如图是函数Q(x)的图象的一部分,设函数f(x)=sinx,g ( x )=| 1 |
| x |
A、
| ||
| B、f(x)g(x) | ||
| C、f(x)-g(x) | ||
| D、f(x)+g(x) |
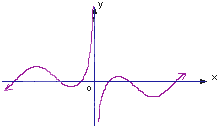 设函数f(x)=sinx,g(x)=
设函数f(x)=sinx,g(x)=