题目内容
在直三棱柱ABC-A1B1C1中,BC1⊥A1C.有下列条件:①AB=AC=BC;②AB⊥AC;③AB=AC.其中能成为BC1⊥AB1的充要条件的是(填上该条件的序号) .
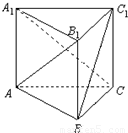
【答案】分析:由题意,对所给的三个条件,结合在直三棱柱ABC-A1B1C1中,BC1⊥A1C.作出如图的图象,借助图象对BC1⊥AB1的充要条件进行研究
解答: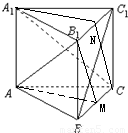 解:若①AB=AC=BC,如图取M,N分别是B1C1,BC的中点,可得AM⊥BC,A1N⊥B1C1,由直三棱柱ABC-A1B1C1中,可得AM,A1N都垂直于侧面B1C1BC,
解:若①AB=AC=BC,如图取M,N分别是B1C1,BC的中点,可得AM⊥BC,A1N⊥B1C1,由直三棱柱ABC-A1B1C1中,可得AM,A1N都垂直于侧面B1C1BC,
由此知AM,A1N都垂直于线BC1,又BC1⊥A1C.结合图形知BC1⊥CN
又由M,N是中点及直三棱柱的性质知B1M∥CN,故可得BC1⊥B1M,
再结合AM垂直于线BC1,及图形知BC1⊥面AMB1,
故有BC1⊥AB1,
故①能成为BC1⊥AB1的充要条件
同理③也可
对于条件②,其不能证得BC1⊥AB1,故不为BC1⊥AB1的充要条件
综上①③符合题意
故答案为①③
点评:本题考查空间中直线与直线之间的位置关系,解题的关键是构造图形证明线面垂直从而证明线线垂直.利用线面垂直证明线线垂直是立体几何中证明线线垂直常用的方法.
解答:
 解:若①AB=AC=BC,如图取M,N分别是B1C1,BC的中点,可得AM⊥BC,A1N⊥B1C1,由直三棱柱ABC-A1B1C1中,可得AM,A1N都垂直于侧面B1C1BC,
解:若①AB=AC=BC,如图取M,N分别是B1C1,BC的中点,可得AM⊥BC,A1N⊥B1C1,由直三棱柱ABC-A1B1C1中,可得AM,A1N都垂直于侧面B1C1BC,由此知AM,A1N都垂直于线BC1,又BC1⊥A1C.结合图形知BC1⊥CN
又由M,N是中点及直三棱柱的性质知B1M∥CN,故可得BC1⊥B1M,
再结合AM垂直于线BC1,及图形知BC1⊥面AMB1,
故有BC1⊥AB1,
故①能成为BC1⊥AB1的充要条件
同理③也可
对于条件②,其不能证得BC1⊥AB1,故不为BC1⊥AB1的充要条件
综上①③符合题意
故答案为①③
点评:本题考查空间中直线与直线之间的位置关系,解题的关键是构造图形证明线面垂直从而证明线线垂直.利用线面垂直证明线线垂直是立体几何中证明线线垂直常用的方法.

练习册系列答案
相关题目
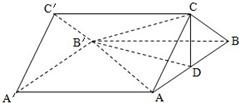 如图,在直三棱柱ABC-A′B′C′中,已知AA′=4,AC=BC=2,∠ACB=90°,D是AB的中点.
如图,在直三棱柱ABC-A′B′C′中,已知AA′=4,AC=BC=2,∠ACB=90°,D是AB的中点. (2012•泸州一模)如图,在直三棱柱ABC-A′B′C′中,AB=BC=CA=a,
(2012•泸州一模)如图,在直三棱柱ABC-A′B′C′中,AB=BC=CA=a, 如图,在直三棱柱ABC-A′B′C′中,AA′=AB=BC=1,∠ABC=90°.棱A′C′上有两个动点E,F,且EF=a (a为常数).
如图,在直三棱柱ABC-A′B′C′中,AA′=AB=BC=1,∠ABC=90°.棱A′C′上有两个动点E,F,且EF=a (a为常数). 如图所示,在直三棱柱ABC-A′B′C′中,∠BAC=90°,AB=BB′=1,直线B′C与平面ABC成30°角.
如图所示,在直三棱柱ABC-A′B′C′中,∠BAC=90°,AB=BB′=1,直线B′C与平面ABC成30°角. 如图,在直三棱柱ABC-A′B′C′中,点D是BC的中点,∠ACB=90°,AC=BC=1,AA′=2,
如图,在直三棱柱ABC-A′B′C′中,点D是BC的中点,∠ACB=90°,AC=BC=1,AA′=2,