题目内容
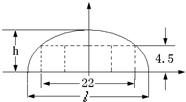 如图,某隧道设计为双向四车道,车道总宽22米,要求通行车辆限高4.5米,隧道全长2.5千米,隧道的拱线近似地看成半个椭圆形状.
如图,某隧道设计为双向四车道,车道总宽22米,要求通行车辆限高4.5米,隧道全长2.5千米,隧道的拱线近似地看成半个椭圆形状.(1)若最大拱高h为6米,则隧道设计的拱宽l是多少?
(2)若最大拱高h不小于6米,则应如何设计拱高h和拱宽l,才能使半个椭圆形隧道的土方工程量最最小?(半个椭圆的面积公式为S=
| π | 4 |
分析:(1)根据题意,建立坐标系,可得P的坐标并设出椭圆的方程,将b=h=6与点P坐标代入椭圆方程,得a=
,依题意,可得l=2a,计算可得答案;
(2)根据题意,设椭圆方程为
+
=1,将(11,4.5)代入方程可得
+
=1,结合基本不等式可得
+
≥
,分析可得当ab≥99且l=2a,h=b时,S=
lh=
≥
,进而分析可得答案.
44
| ||
| 7 |
(2)根据题意,设椭圆方程为
| x2 |
| a2 |
| y2 |
| b2 |
| 112 |
| a2 |
| 4.52 |
| b2 |
| 112 |
| a2 |
| 4.52 |
| b2 |
| 2×11×4.5 |
| ab |
| π |
| 4 |
| πab |
| 2 |
| 99π |
| 2 |
解答: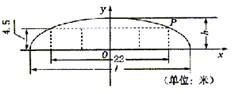 解:(1)如图建立直角坐标系,则点P(11,4.5),
解:(1)如图建立直角坐标系,则点P(11,4.5),
椭圆方程为
+
=1.
将b=h=6与点P坐标代入椭圆方程,
得a=
,
此时此时l=2a=
≈33.3
因此隧道的拱宽约为33.3米;
(2)由椭圆方程
+
=1,
根据题意,将(11,4.5)代入方程可得
+
=1.
因为
+
≥
即ab≥99且l=2a,h=b,
所以S=
lh=
≥
当S取最小值时,
有
=
=
,
得a=11
,b=
此时l=2a=22
≈31.1,h=b≈6.4
故当拱高约为6.4米、拱宽约为31.1米时,土方工程量最小.
 解:(1)如图建立直角坐标系,则点P(11,4.5),
解:(1)如图建立直角坐标系,则点P(11,4.5),椭圆方程为
| x2 |
| a2 |
| y2 |
| b2 |
将b=h=6与点P坐标代入椭圆方程,
得a=
44
| ||
| 7 |
此时此时l=2a=
88
| ||
| 7 |
因此隧道的拱宽约为33.3米;
(2)由椭圆方程
| x2 |
| a2 |
| y2 |
| b2 |
根据题意,将(11,4.5)代入方程可得
| 112 |
| a2 |
| 4.52 |
| b2 |
因为
| 112 |
| a2 |
| 4.52 |
| b2 |
| 2×11×4.5 |
| ab |
即ab≥99且l=2a,h=b,
所以S=
| π |
| 4 |
| πab |
| 2 |
| 99π |
| 2 |
当S取最小值时,
有
| 112 |
| a2 |
| 4.52 |
| b2 |
| 1 |
| 2 |
得a=11
| 2 |
9
| ||
| 2 |
此时l=2a=22
| 2 |
故当拱高约为6.4米、拱宽约为31.1米时,土方工程量最小.
点评:本题考查椭圆的实际运用,注意与实际问题相结合,建立合适的坐标系,设出点的坐标,结合椭圆的有关性质进行分析、计算、解题.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
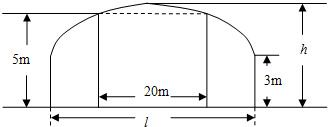
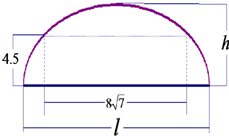 如图,某隧道设计为双向四车道,车道总宽为
如图,某隧道设计为双向四车道,车道总宽为
