题目内容
函数y=kx+b，其中k，b是常数，其图象是一条直线，称这个函数为线性函数，而对于非线性可导函数f（x），在已知点x附近一点x的函数值f（x）可以用下面方法求其近似代替值，f（x），利≈f（x）+f′（x）（x-x0）用这一方法，对于实数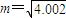
，取x的值为4，则m的近似代替值是 ．
【答案】分析：由题意可令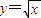
，对函数求导，求出x=4的切线方程，然后求出x=4.002时y的近视解即可
解答：解：令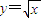
，
∴
=
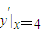∴y=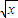
在x=4处的切线为y-2=
（x-4）即
，
∴
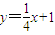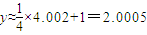
故答案为：2.005
点评：本题主要考查了函数的导数在切线斜率求解中的应用，解题的关键是准确应用题目中的定义
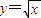，对函数求导，求出x=4的切线方程，然后求出x=4.002时y的近视解即可解答：解：令
，∴
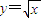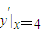=∴y=
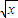在x=4处的切线为y-2=（x-4）即，∴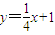
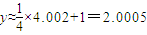
故答案为：2.005
点评：本题主要考查了函数的导数在切线斜率求解中的应用，解题的关键是准确应用题目中的定义
练习册系列答案
相关题目