题目内容

如图,已知等腰△ABC的底边BC=3,顶角为120°,D是BC边上一点,且BD=1.把△ADC沿AD折起,使得平面CAD⊥平面ABD,连接BC形成三棱锥C-ABD.
(Ⅰ) ①求证:AC⊥平面ABD;②求三棱锥C-ABD的体积;
(Ⅱ) 求AC与平面BCD所成的角的正弦值.
分析:(I)①由已知中等腰△ABC的底边BC=3,顶角为120°,BD=1,我们易根据勾股定理得到AC⊥AD,再由平面ADC⊥平面ABD,结合面面垂直的性质,即可得到AC⊥平面ABD;②根据①的结论,计算出三棱锥C-ABD的底面面积和高,代入棱锥体积公式,即可得到答案.
(II)在作等腰△ABC底边上的高线AE,点E为垂足,连接CE,作AH⊥CE于点H,则∠ACH是直线AC与平面BCD所成的角,解三角形ACH即可得到AC与平面BCD所成的角的正弦值.
解答:解:(Ⅰ)①由已知得,∠B=∠C=30°,
AB=AC=.
在△ABD中,由BD=1,得AD=
=1,(3分)
在△ACD中,∵AC
2+AD
2=4=CD
2,∴AC⊥AD.
平面ADC⊥平面ABD,∴AC⊥平面ABD.(5分)
②∵AC⊥平面ABD,∴V
C-ABD=
•S△ABD•AC=
•(•1•sin30°)•=.(8分)
(Ⅱ)
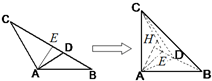
由BD=1,得CD=2,
在平面内作等腰△ABC底边上的高线AE,点E为垂足,则AE=
.
在三棱锥C-ABD中,连接CE,作AH⊥CE于点H,
∵BD⊥AC,BD⊥AE,∴BD⊥平面ACE,
∵AH?平面ACE,∴BD⊥AH,∴AH⊥平面BCD,
∴∠ACH是直线AC与平面BCD所成的角.(11分)
在Rt△ACE中,得
CE=,
AH==
,
∴
sin∠ACH═,即直线AC与平面BCE所成的角的正弦值为
.(14分)
点评:本题考查的知识点是直线与平面所成的角,棱锥的体积,直线与平面垂直的判定,(I)的关键是根据面面垂直的性质得到线面垂直,(2)的关键是找出直线与平面夹角的平面角.
练习册系列答案
相关题目
 如图,已知等腰△ABC的底边BC=3,顶角为120°,D是BC边上一点,且BD=1.把△ADC沿AD折起,使得平面CAD⊥平面ABD,连接BC形成三棱锥C-ABD.
如图,已知等腰△ABC的底边BC=3,顶角为120°,D是BC边上一点,且BD=1.把△ADC沿AD折起,使得平面CAD⊥平面ABD,连接BC形成三棱锥C-ABD. 由BD=1,得CD=2,
由BD=1,得CD=2, 由BD=1,得CD=2,
由BD=1,得CD=2,
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
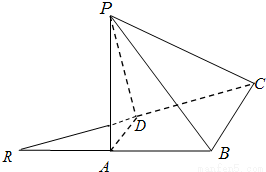
小学同步三练核心密卷系列答案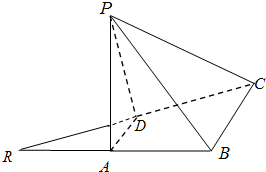 如图,已知等腰直角三角形RBC,其中∠RBC=90°,RB=BC=2.点A、D分别是RB、RC的中点,现将△RAD沿着边AD折起到△PAD位置,使PA⊥AB,连接PB、PC.
如图,已知等腰直角三角形RBC,其中∠RBC=90°,RB=BC=2.点A、D分别是RB、RC的中点,现将△RAD沿着边AD折起到△PAD位置,使PA⊥AB,连接PB、PC.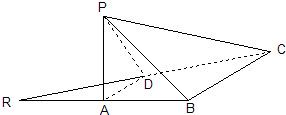 如图,已知等腰直角三角形RBC,其中∠RBC=90°,RB=BC=2.点A、D分别是RB、RC的中点,现将△RAD沿着边AD折起到△PAD位置,使PA⊥AB,连接PB、PC.
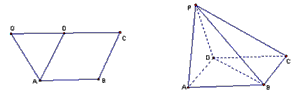
如图,已知等腰直角三角形RBC,其中∠RBC=90°,RB=BC=2.点A、D分别是RB、RC的中点,现将△RAD沿着边AD折起到△PAD位置,使PA⊥AB,连接PB、PC.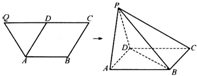 如图,已知等腰梯形ABCQ,AB∥CQ,CQ=2AB=2BC=4,D是CQ的中点,∠BCQ=60°,将△QDA沿AD折起,点Q变为点P,使平面PAD⊥平面ABCD.
如图,已知等腰梯形ABCQ,AB∥CQ,CQ=2AB=2BC=4,D是CQ的中点,∠BCQ=60°,将△QDA沿AD折起,点Q变为点P,使平面PAD⊥平面ABCD.