题目内容
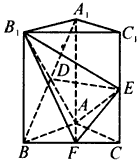
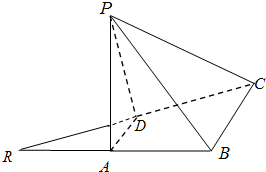 如图,已知等腰直角三角形RBC,其中∠RBC=90°,RB=BC=2.点A、D分别是RB、RC的中点,现将△RAD沿着边AD折起到△PAD位置,使PA⊥AB,连接PB、PC.
如图,已知等腰直角三角形RBC,其中∠RBC=90°,RB=BC=2.点A、D分别是RB、RC的中点,现将△RAD沿着边AD折起到△PAD位置,使PA⊥AB,连接PB、PC.(1)求证:BC⊥PB;
(2)求二面角A-CD-P的平面角的余弦值.
分析:(1)证明BC⊥PB,一般先证明线面垂直即找到一个平面包含其中一条直线而另一条直线与此平面垂直,即可证明线线垂直.
(2)取RD的中点F,连接AF、PF.∵RA=AD=1,∴AF⊥RC.根据题意可证明RC⊥平面PAF,因为PF?平面PAF,所以RC⊥PF.所以∠AFP是二面角A-CD-P的平面角.再结合解三角形的一个知识求出答案即可.
(2)取RD的中点F,连接AF、PF.∵RA=AD=1,∴AF⊥RC.根据题意可证明RC⊥平面PAF,因为PF?平面PAF,所以RC⊥PF.所以∠AFP是二面角A-CD-P的平面角.再结合解三角形的一个知识求出答案即可.
解答:解:(1)∵点A、D分别是RB、RC的中点,
∴AD∥BC,AD=
BC.
∴∠PAD=∠RAD=∠RBC=90°.
∴PA⊥AD.
∴PA⊥BC,
∵BC⊥AB,PA∩AB=A,
∴BC⊥平面PAB.
∵PB?平面PAB,
∴BC⊥PB.
(2)取RD的中点F,连接AF、PF.
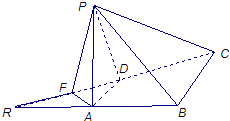 ∵RA=AD=1,
∵RA=AD=1,
∴AF⊥RC.
∵AP⊥AR,AP⊥AD,
∴AP⊥平面RBC.
∵RC?平面RBC,
∴RC⊥AP
∵AF∩AP=A,
∴RC⊥平面PAF.
∵PF?平面PAF,
∴RC⊥PF.
∴∠AFP是二面角A-CD-P的平面角.
在Rt△RAD中,AF=
RD=
=
,
在Rt△PAF中,PF=
=
,cos∠AFP=
=
=
.
∴二面角A-CD-P的平面角的余弦值是
.
∴AD∥BC,AD=
| 1 |
| 2 |
∴∠PAD=∠RAD=∠RBC=90°.
∴PA⊥AD.
∴PA⊥BC,
∵BC⊥AB,PA∩AB=A,
∴BC⊥平面PAB.
∵PB?平面PAB,
∴BC⊥PB.
(2)取RD的中点F,连接AF、PF.
 ∵RA=AD=1,
∵RA=AD=1,∴AF⊥RC.
∵AP⊥AR,AP⊥AD,
∴AP⊥平面RBC.
∵RC?平面RBC,
∴RC⊥AP
∵AF∩AP=A,
∴RC⊥平面PAF.
∵PF?平面PAF,
∴RC⊥PF.
∴∠AFP是二面角A-CD-P的平面角.
在Rt△RAD中,AF=
| 1 |
| 2 |
| 1 |
| 2 |
| RA2+AD2 |
| ||
| 2 |
在Rt△PAF中,PF=
| PA2+AF2 |
| ||
| 2 |
| AF |
| PF |
| ||||
|
| ||
| 3 |
∴二面角A-CD-P的平面角的余弦值是
| ||
| 3 |
点评:解决此类问题的关键是熟悉几何体的结构特征,熟练进行线线垂直与线面垂直的转化,主要考查学生的空间想象能力与推理论证能力.

练习册系列答案
相关题目
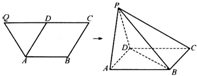 如图,已知等腰梯形ABCQ,AB∥CQ,CQ=2AB=2BC=4,D是CQ的中点,∠BCQ=60°,将△QDA沿AD折起,点Q变为点P,使平面PAD⊥平面ABCD.
如图,已知等腰梯形ABCQ,AB∥CQ,CQ=2AB=2BC=4,D是CQ的中点,∠BCQ=60°,将△QDA沿AD折起,点Q变为点P,使平面PAD⊥平面ABCD.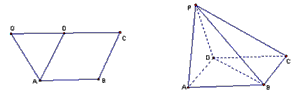
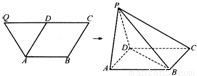 如图,已知等腰梯形ABCQ,AB∥CQ,CQ=2AB=2BC=4,D是CQ的中点,∠BCQ=60°,将△QDA沿AD折起,点Q变为点P,使平面PAD⊥平面ABCD.
如图,已知等腰梯形ABCQ,AB∥CQ,CQ=2AB=2BC=4,D是CQ的中点,∠BCQ=60°,将△QDA沿AD折起,点Q变为点P,使平面PAD⊥平面ABCD.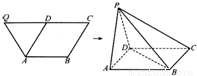 如图,已知等腰梯形ABCQ,AB∥CQ,CQ=2AB=2BC=4,D是CQ的中点,∠BCQ=60°,将△QDA沿AD折起,点Q变为点P,使平面PAD⊥平面ABCD.
如图,已知等腰梯形ABCQ,AB∥CQ,CQ=2AB=2BC=4,D是CQ的中点,∠BCQ=60°,将△QDA沿AD折起,点Q变为点P,使平面PAD⊥平面ABCD.