题目内容
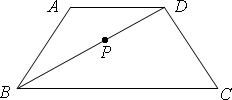
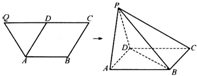 如图,已知等腰梯形ABCQ,AB∥CQ,CQ=2AB=2BC=4,D是CQ的中点,∠BCQ=60°,将△QDA沿AD折起,点Q变为点P,使平面PAD⊥平面ABCD.
如图,已知等腰梯形ABCQ,AB∥CQ,CQ=2AB=2BC=4,D是CQ的中点,∠BCQ=60°,将△QDA沿AD折起,点Q变为点P,使平面PAD⊥平面ABCD.(1)求证:BC∥平面PAD;
(2)求证:△PBC是直角三角形;
(3)求三棱锥P-BCD的体积.
分析:(1)欲证BC∥平面PAD,根据直线与平面平行的判定定理可知只需证BC与平面PAD内一直线平行,易证ABCD是平行四边形,则BC∥AD.又BC?平面PAD,AD?平面PAD,满足定理所需条件;
(2)由题意可知ABCD是菱形,取AD中点E,连PE,BE,根据面面垂直的性质定理可知PE⊥平面ABCD,则PE⊥BC.又BC∥AD,从而BC⊥BE.又PE∩BE=E,根据线面垂直的判定定理可知BC⊥平面PEB,则BC⊥PB,从而得到结论;
(3)先求出PE,三角形BCD的面积,然后利用三棱锥的体积公式进行求解即可.
(2)由题意可知ABCD是菱形,取AD中点E,连PE,BE,根据面面垂直的性质定理可知PE⊥平面ABCD,则PE⊥BC.又BC∥AD,从而BC⊥BE.又PE∩BE=E,根据线面垂直的判定定理可知BC⊥平面PEB,则BC⊥PB,从而得到结论;
(3)先求出PE,三角形BCD的面积,然后利用三棱锥的体积公式进行求解即可.
解答:解: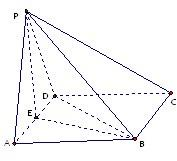 (1)证明:∵AB∥CQ,D是CQ的中点,
(1)证明:∵AB∥CQ,D是CQ的中点,
∴AB∥CD,AB=CD,∴ABCD是平行四边形,∴BC∥AD.
又∵BC?平面PAD,AD?平面PAD,∴BC∥平面PAD.
(2)∵∠BCQ=60°,AB=BC,
∴ABCD是菱形,∴△PDA,△BDA均为等边三角形.
取AD中点E,连PE,BE.∴PE⊥AD,BE⊥AD.又∵平面PAD⊥平面ABCD,交线为AD,
∴PE⊥平面ABCD,∴PE⊥BC.
又∵BC∥AD,∴BC⊥BE.又∵PE∩BE=E,
∴BC⊥平面PEB,∴BC⊥PB.
∴△PBC是直角三角形.
(3)∵PE=
AD=
,s△BCD=
×22=
.
∴VP-BCD=
S△BCD•PE=
×
×
=1,
∴三棱锥P-BCD的体积为1.
 (1)证明:∵AB∥CQ,D是CQ的中点,
(1)证明:∵AB∥CQ,D是CQ的中点,∴AB∥CD,AB=CD,∴ABCD是平行四边形,∴BC∥AD.
又∵BC?平面PAD,AD?平面PAD,∴BC∥平面PAD.
(2)∵∠BCQ=60°,AB=BC,
∴ABCD是菱形,∴△PDA,△BDA均为等边三角形.
取AD中点E,连PE,BE.∴PE⊥AD,BE⊥AD.又∵平面PAD⊥平面ABCD,交线为AD,
∴PE⊥平面ABCD,∴PE⊥BC.
又∵BC∥AD,∴BC⊥BE.又∵PE∩BE=E,
∴BC⊥平面PEB,∴BC⊥PB.
∴△PBC是直角三角形.
(3)∵PE=
| ||
| 2 |
| 3 |
| ||
| 4 |
| 3 |
∴VP-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 3 |
∴三棱锥P-BCD的体积为1.
点评:本题主要考查了线面平行的判定,以及线面垂直的性质和三棱锥体积的计算,同时考查了空间想象能力、转化与划归的思想,属于基础题.

练习册系列答案
相关题目
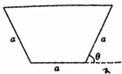 汶川大地震后,为了消除某堰塞湖可能造成的危险,救授指挥部商定,给该堰塞湖挖一个横截面为等腰梯形的简易引水槽(如图所示)进行引流,已知等腰梯形的下底与腰的长度都为a,且水槽的单位时间内的最大流量与横载面的面积为正比,比例系数k>0.
汶川大地震后,为了消除某堰塞湖可能造成的危险,救授指挥部商定,给该堰塞湖挖一个横截面为等腰梯形的简易引水槽(如图所示)进行引流,已知等腰梯形的下底与腰的长度都为a,且水槽的单位时间内的最大流量与横载面的面积为正比,比例系数k>0.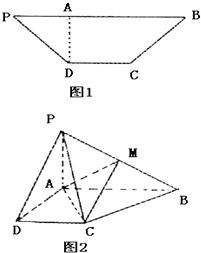 已知等腰梯形PDCB中(如图1),PB=3,DC=1,PB=BC=
已知等腰梯形PDCB中(如图1),PB=3,DC=1,PB=BC= 如图,已知ABCD是底角为30°的等腰梯形,AD=2
如图,已知ABCD是底角为30°的等腰梯形,AD=2 如图,已知A(-2,0),B(2,0),等腰梯形ABCD满足|AB|=-2|CD|,E为AC上一点,且
如图,已知A(-2,0),B(2,0),等腰梯形ABCD满足|AB|=-2|CD|,E为AC上一点,且