题目内容
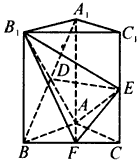
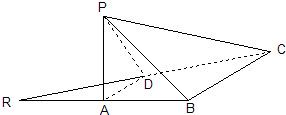 如图,已知等腰直角三角形RBC,其中∠RBC=90°,RB=BC=2.点A、D分别是RB、RC的中点,现将△RAD沿着边AD折起到△PAD位置,使PA⊥AB,连接PB、PC.
如图,已知等腰直角三角形RBC,其中∠RBC=90°,RB=BC=2.点A、D分别是RB、RC的中点,现将△RAD沿着边AD折起到△PAD位置,使PA⊥AB,连接PB、PC.(1)求证:PB⊥BC;
(2)在线段PB上找一点E,使AE∥平面PCD;
(3)求二面角A-CD-P的余弦值.
分析:(1)欲证BC⊥PB,先证BC⊥平面PAB,可证PA⊥BC,PA∩AB=A,BC⊥BA,根据线面垂直的判定定理可证得;
(2)取线段PB的中点E,连接AE,PR,可证得AE∥平面PRC,平面PRC即是平面PDC;
(3)取RD的中点F,连接AF、PF,可证∠AFP是二面角A-CD-P的平面角,在三角形AFP中求出∠AFP的余弦值即可.
(2)取线段PB的中点E,连接AE,PR,可证得AE∥平面PRC,平面PRC即是平面PDC;
(3)取RD的中点F,连接AF、PF,可证∠AFP是二面角A-CD-P的平面角,在三角形AFP中求出∠AFP的余弦值即可.
解答: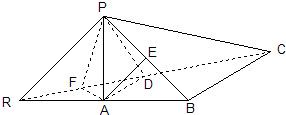 解:(1)∵点A、D分别是RB、RC的中点,
解:(1)∵点A、D分别是RB、RC的中点,
∴AD∥
BC.(1分)
∴∠PAD=∠RAD=∠RBC=90°,
∴PA⊥AD,
∴PA⊥BC.(2分)
又∵PA∩AB=A,BC⊥BA,
∴BC⊥平面PAB,(3分)
∴BC⊥PB.(4分)
(2)取线段PB的中点E,连接AE,PR.(5分)
显然,平面PAB∩平面PCD=PR.
∵RA=BA,BE=PE,
∴AE∥PR.(6分)
又∵AE?平面PRC,
∴AE∥平面PRC(即平面PDC),(7分)
故线段PB的中点E是符合题意要求的点.(8分)
(3)取RD的中点F,连接AF、PF.(9分)
∵RA=AD=1,AP⊥AR且AP⊥AD,AP=1,
∴PR=PD=
,
∴AF⊥DR,PF⊥DR,
∴∠AFP是二面角A-CD-P的平面角.(11分)
∵DR=
,
∴AF=
,PF=
,
∴cos∠AFP=
 解:(1)∵点A、D分别是RB、RC的中点,
解:(1)∵点A、D分别是RB、RC的中点,∴AD∥
| 1 |
| 2 |
∴∠PAD=∠RAD=∠RBC=90°,
∴PA⊥AD,
∴PA⊥BC.(2分)
又∵PA∩AB=A,BC⊥BA,
∴BC⊥平面PAB,(3分)
∴BC⊥PB.(4分)
(2)取线段PB的中点E,连接AE,PR.(5分)
显然,平面PAB∩平面PCD=PR.
∵RA=BA,BE=PE,
∴AE∥PR.(6分)
又∵AE?平面PRC,
∴AE∥平面PRC(即平面PDC),(7分)
故线段PB的中点E是符合题意要求的点.(8分)
(3)取RD的中点F,连接AF、PF.(9分)
∵RA=AD=1,AP⊥AR且AP⊥AD,AP=1,
∴PR=PD=
| 2 |
∴AF⊥DR,PF⊥DR,
∴∠AFP是二面角A-CD-P的平面角.(11分)
∵DR=
| 2 |
∴AF=
| ||
| 2 |
| ||
| 2 |
∴cos∠AFP=
| ||
| 3 |
点评:本题主要考查了平面与平面之间的位置关系,考查空间想象能力、运算能力和推理论证能力,属于基础题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
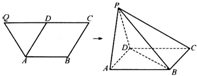 如图,已知等腰梯形ABCQ,AB∥CQ,CQ=2AB=2BC=4,D是CQ的中点,∠BCQ=60°,将△QDA沿AD折起,点Q变为点P,使平面PAD⊥平面ABCD.
如图,已知等腰梯形ABCQ,AB∥CQ,CQ=2AB=2BC=4,D是CQ的中点,∠BCQ=60°,将△QDA沿AD折起,点Q变为点P,使平面PAD⊥平面ABCD.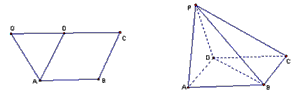
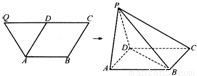 如图,已知等腰梯形ABCQ,AB∥CQ,CQ=2AB=2BC=4,D是CQ的中点,∠BCQ=60°,将△QDA沿AD折起,点Q变为点P,使平面PAD⊥平面ABCD.
如图,已知等腰梯形ABCQ,AB∥CQ,CQ=2AB=2BC=4,D是CQ的中点,∠BCQ=60°,将△QDA沿AD折起,点Q变为点P,使平面PAD⊥平面ABCD.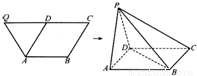 如图,已知等腰梯形ABCQ,AB∥CQ,CQ=2AB=2BC=4,D是CQ的中点,∠BCQ=60°,将△QDA沿AD折起,点Q变为点P,使平面PAD⊥平面ABCD.
如图,已知等腰梯形ABCQ,AB∥CQ,CQ=2AB=2BC=4,D是CQ的中点,∠BCQ=60°,将△QDA沿AD折起,点Q变为点P,使平面PAD⊥平面ABCD.