题目内容
(本小题满分10分)选修4-1:几何证明选讲
如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E、D,连结EC、CD.

(Ⅰ)求证:直线AB是⊙O的切线;
(Ⅱ)若tan∠CED= ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长.
如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E、D,连结EC、CD.

(Ⅰ)求证:直线AB是⊙O的切线;
(Ⅱ)若tan∠CED=
 ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长.分10分)
解:(Ⅰ)如图,连接OC,∵OA=OB,CA=CB ∴OC⊥AB
∴AB是⊙O的切线…………4分
(Ⅱ)∵ED是直径,∴∠ECD=90°∴∠E+∠EDC=90°
又∵∠BCD+∠OCD=90°,∠OCD=∠ODC,∴∠BCD=∠E
又∵∠ CBD+∠EBC,∴△BCD∽△BEC
CBD+∠EBC,∴△BCD∽△BEC
∴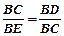 ∴BC2=BD•BE
∴BC2=BD•BE
∵tan∠CED=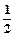 ,∴
,∴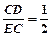
∵△BCD∽△BEC, ∴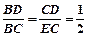 …………8分
…………8分
设BD=x,则BC=2x
又BC2=BD•BE,∴(2x)2=x•(x+6)
解得:x1=0,x2="2," ∵BD=x>0, ∴BD=2
∴OA=OB=BD+OD=3+ 2=5…………10分
2=5…………10分
解:(Ⅰ)如图,连接OC,∵OA=OB,CA=CB ∴OC⊥AB
∴AB是⊙O的切线…………4分
(Ⅱ)∵ED是直径,∴∠ECD=90°∴∠E+∠EDC=90°
又∵∠BCD+∠OCD=90°,∠OCD=∠ODC,∴∠BCD=∠E
又∵∠
 CBD+∠EBC,∴△BCD∽△BEC
CBD+∠EBC,∴△BCD∽△BEC∴
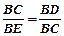 ∴BC2=BD•BE
∴BC2=BD•BE∵tan∠CED=
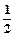 ,∴
,∴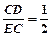
∵△BCD∽△BEC, ∴
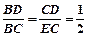 …………8分
…………8分设BD=x,则BC=2x
又BC2=BD•BE,∴(2x)2=x•(x+6)
解得:x1=0,x2="2," ∵BD=x>0, ∴BD=2
∴OA=OB=BD+OD=3+
 2=5…………10分
2=5…………10分略

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 :
:  ,圆C:
,圆C:  .
. 到点F的距离比它到直线
到点F的距离比它到直线 的最大值和最小值;
的最大值和最小值;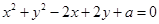 表示圆,则实数
表示圆,则实数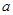 的取值范围是( )
的取值范围是( )



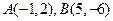 为直径两端点的圆的方程。(8分)
为直径两端点的圆的方程。(8分) 为圆
为圆 的两条相互垂直的弦,垂足为
的两条相互垂直的弦,垂足为 ,则四边形
,则四边形 的面积的最大值为
的面积的最大值为 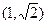 的直线l将圆
的直线l将圆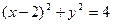 分成两段弧,当劣弧所对的圆心角最小时,求直线l的斜率。
分成两段弧,当劣弧所对的圆心角最小时,求直线l的斜率。 +
+ -4x=0外一点P(m,n)作圆的两条切线,当这两条切线互相垂直时,m,n 应满足的关系式为( )
-4x=0外一点P(m,n)作圆的两条切线,当这两条切线互相垂直时,m,n 应满足的关系式为( ) +
+  ="4"
="4"  +
+