题目内容
如果n的展开式中含有非零常数项，则正整数n的最小值为( )
| A．3 | B．5 |
| C．6 | D．10 |
B
分析：利用二项展开式的通项公式求出第r+1项，令x的指数为0得方程，求使方程有整数解的最小n值即可．
解：由展开式通项有Tr+1=
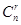(3x2)n-r(-
)r=Cnr?3n-r?（-2）r?x2n-5r由题意得2n-5r=0?n=
r(r=0，1，2，，n)，故当r=2时，正整数n的最小值为5，
故选项为B
练习册系列答案
相关题目
的四位数？
将A、B、C、D四个维修点的这批配件分别调整为40、45、54
、61件，但调整只能在相邻维修点之间进行．那么要完成上述调整，最少的调动件次(n件配件从一个维修点调整到相邻维修点的调动件次为n)为 .
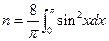
展开式中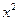
项的系数为__ _