Question

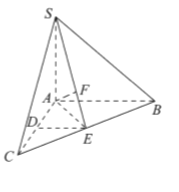
【题目】如图，在四棱锥中：底面ABCD，底面ABCD为梯形，，，且，BC=1，M为棱PD上的点。

（Ⅰ）若，求证：CM∥平面PAB；

（Ⅱ）求证：平面平面PAB；

（Ⅲ）求直线BD与平面PAD所成角的大小.

Answer 1

【答案】（Ⅰ ）见解析（Ⅱ）见解析（Ⅲ）30°

【解析】

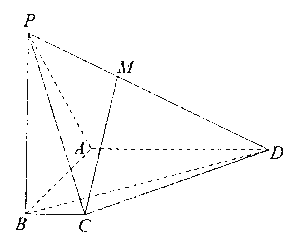
（Ⅰ）过点M作MH∥AD，交PA于H，连接BH，BCMH为平行四边形，CM∥BH,从而得证；

（Ⅱ）要证平面平面PAB，即证；

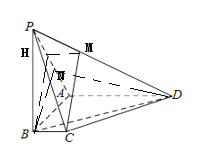
（Ⅲ）取PA的中点为N，连接BN，由（Ⅱ）可知BN⊥平面PAD，即∠BDN为直线BD与平面PAD所成角。

解：（Ⅰ）证明：过点M作MH∥AD，交PA于H，连接BH，

因为，所以．

又MH∥AD，AD∥BC，所以HM∥BC．

所以BCMH为平行四边形，所以CM∥BH．

又BH平面PAB，CM平面PAB，

所以CM∥平面PAB．

（Ⅱ）∵底面ABCD，AD平面ABCD

∴，又，且

∴，又平面PAD

∴平面平面PAB；

（Ⅲ）取PA的中点为N，连接BN，

∵，∴BN⊥PA，连接DN

又平面平面PAB，故BN⊥平面

则∠BDN为直线BD与平面PAD所成角

此时，BN=，BD=

∴sin∠BDN=，即∠BDN=30°

∴求直线BD与平面PAD所成角的大小30°.