题目内容
【题目】已知函数 ,其中
,其中![]() ,
,![]() 是非空数集且
是非空数集且![]() .设
.设![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() ;
;
(2)是否存在实数![]() ,使得
,使得![]() ,且
,且![]() ?若存在,求出所有满足条件的
?若存在,求出所有满足条件的![]() ;若不存在,说明理由;
;若不存在,说明理由;
(3)若![]() 且
且![]() ,
,![]() ,
,![]() 单调递增,求集合
单调递增,求集合![]() ,
,![]() .
.
【答案】(1)![]() ;(2)存在,3;(3)
;(2)存在,3;(3)![]() ,
,![]() ,其中
,其中![]() 或
或![]() ,
,![]() ,其中
,其中![]() 或
或![]() ,
,![]() ,或
,或![]() ,
,![]()
【解析】
(1)依题意![]() 分别表示
分别表示![]() 时
时![]() 的值域,结合
的值域,结合![]() 的图像和性质和二次函数的图像和性质分别求出此分段函数两支上的值域,即可得出结论;
的图像和性质和二次函数的图像和性质分别求出此分段函数两支上的值域,即可得出结论;
(2)抓住线索![]() ,逐层深入,先判断
,逐层深入,先判断![]() ,得
,得![]() 的范围,再由已知推理缩小此范围,最后确定
的范围,再由已知推理缩小此范围,最后确定![]() 的值;
的值;
(3)根据函数的单调性,可得![]() ,再证明在
,再证明在![]() 上存在分界点的话,这个分界点应具有怎样的性质,最后根据此性质写出满足题意的集合
上存在分界点的话,这个分界点应具有怎样的性质,最后根据此性质写出满足题意的集合![]() .
.
(1)![]() ,
,
![]() ,
,
![]() ;
;
(2)若![]() 则
则![]() ,不合题意,
,不合题意,
![]() 从而
从而![]() ,
,
![]() ,得
,得![]() .
.
若![]() ,则
,则![]() ,
,
![]() 的原象
的原象![]() 且
且![]() ,
,
![]() ,矛盾.
,矛盾.
![]() ,此时可取
,此时可取![]() ,满足题意.
,满足题意.
(3)![]() 是单调递增函数,
是单调递增函数,![]() 对任意
对任意![]() ,
,
![]() ,同理可得:
,同理可得:![]() .
.
若存在![]() ,使得
,使得![]() 则
则![]() ,
,
于是![]() ,记
,记![]() ,
,
![]() ,同理可知
,同理可知![]() ,由
,由![]() ,
,
得![]() ,
,
![]() ,
,
对于任意![]() ,取
,取![]()
中的自然数![]() ,则
,则![]()
综上所述,满足条件的![]() 必有如下表示:
必有如下表示:
![]() ,其中
,其中![]() ,
,
或![]() ,其中
,其中![]() ,
,
或![]() ,或
,或![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了丰富学生的课外文化生活,某中学积极探索开展课外文体活动的新途径及新形式,取得了良好的效果.为了调查学生的学习积极性与参加文体活动是否有关,学校对200名学生做了问卷调查,列联表如下:
参加文体活动 | 不参加文体活动 | 合计 | |
学习积极性高 | 80 | ||
学习积极性不高 | 60 | ||
合计 | 200 |
已知在全部200人中随机抽取1人,抽到学习积极性不高的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有99.9%的把握认为学习积极性高与参加文体活动有关?请说明你的理由;
(3)若从不参加文体活动的同学中按照分层抽样的方法选取5人,再从所选出的5人中随机选取2人,求至少有1人学习积极性不高的概率.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
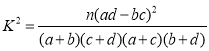 ,其中
,其中![]() .
.
【题目】“中国式过马路”的大意是凑够一撮人即可走,跟红绿灯无关.部分法律专家的观点为“交通规则的制定目的就在于服务城市管理,方便行人,而‘中国式过马路’是对我国法治化进程的严重阻碍,反应了国人规则意识的淡薄.”某新闻媒体对此观点进行了网上调查,所有参与调查的人中,持“支持”“中立”和“不支持”态度的人数如表所示:
支持 | 中立 | 不支持 | |
20岁以下 | 800 | 450 | 200 |
20岁及以上 | 100 | 150 | 300 |
在所有参与调查的人中,用分层随机抽样的方法抽取![]() 人,已知从持“支持”态度的人抽取了45人,则
人,已知从持“支持”态度的人抽取了45人,则![]() ______.
______.