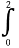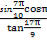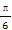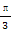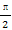Question

定义F(x,y)=(1+x)y,x,y∈(0,+∞).令函数f(x)=F(1,log2(x2-4x+9))的图象为曲线C1,曲线C1与y轴交于点A(0,m),过坐标原点O向曲线C1作切线,切点为B(n,t)(n>0),设曲线C1在点A,B之间的曲线段与线段OA,OB所围成图形的面积为S,求S的值.

 

 

Answer 1

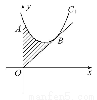
9

【解析】因为F(x,y)=(1+x)y,所以f(x)=F(1,log2(x2-4x+9))=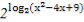=x2-4x+9,故A(0,9),又过坐标原点O向曲线C1作切线,切点为B(n,t)(n>0),f'(x)=2x-4.

所以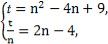解得B(3,6),

所以S=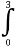(x2-4x+9-2x)dx

=(-3x2+9x)=9.