题目内容
已知椭圆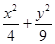 =1上任一点P,由点P向x轴作垂线PQ,垂足为Q,设点M在PQ上,且
=1上任一点P,由点P向x轴作垂线PQ,垂足为Q,设点M在PQ上,且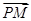 =2
=2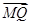 ,点M的轨迹为C.
,点M的轨迹为C.
(1)求曲线C的方程;
(2)过点D(0,-2)作直线l与曲线C交于A、B两点,设N是过点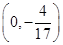 且平行于x轴的直线上一动点,且满足
且平行于x轴的直线上一动点,且满足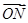 =
=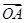 +
+ (O为原点),且四边形OANB为矩形,求直线l的方程.
(O为原点),且四边形OANB为矩形,求直线l的方程.
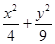 =1上任一点P,由点P向x轴作垂线PQ,垂足为Q,设点M在PQ上,且
=1上任一点P,由点P向x轴作垂线PQ,垂足为Q,设点M在PQ上,且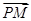 =2
=2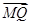 ,点M的轨迹为C.
,点M的轨迹为C.(1)求曲线C的方程;
(2)过点D(0,-2)作直线l与曲线C交于A、B两点,设N是过点
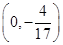 且平行于x轴的直线上一动点,且满足
且平行于x轴的直线上一动点,且满足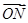 =
=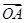 +
+ (O为原点),且四边形OANB为矩形,求直线l的方程.
(O为原点),且四边形OANB为矩形,求直线l的方程.(1)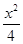 +y2=1(2)y=±2x-2.
+y2=1(2)y=±2x-2.
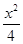 +y2=1(2)y=±2x-2.
+y2=1(2)y=±2x-2.(1)设点M(x,y)是曲线C上任意一点,
∵PM⊥x轴,且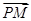 =2
=2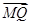 ,
,
所以点P的坐标为(x,3y),
又点P在椭圆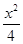 +
+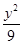 =1上,所以
=1上,所以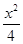 +
+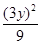 =1,
=1,
因此曲线C的方程是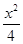 +y2=1.
+y2=1.
(2)当直线l的斜率不存在时,显然不满足条件,所以设直线l的方程为y=kx-2,直线l与椭圆交于A(x1,y1),B(x2,y2)两点.
由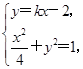 得(1+4k2)x2-16kx+12=0,
得(1+4k2)x2-16kx+12=0,
依题意Δ=(16k)2-48(1+4k2)>0,得k2>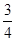 (*),
(*),
此时x1+x2=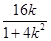 ,x1x2=
,x1x2=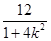 .
.
因为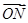 =
=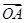 +
+ ,所以四边形OANB为平行四边形.
,所以四边形OANB为平行四边形.
又四边形OANB是矩形,所以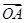 ·
· =0,
=0,
即x1x2+y1y2=x1x2+k2x1x2-2k(x1+x2)+4=(1+k2)x1x2-2k(x1+x2)+4=0,
∴(1+k2)·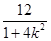 -2k·
-2k·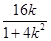 +4=0,
+4=0,
解之得k2=4,∴k=±2.满足(*)式.
设N(x0,y0),由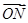 =
=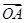 +
+ ,得
,得
y0=y1+y2=k(x1+x2)-4=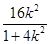 -4=-
-4=- ,
,
从而点N在直线y=- 上,满足题设,
上,满足题设,
故直线l的方程为y=±2x-2.
∵PM⊥x轴,且
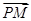 =2
=2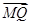 ,
,所以点P的坐标为(x,3y),
又点P在椭圆
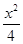 +
+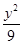 =1上,所以
=1上,所以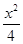 +
+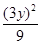 =1,
=1,因此曲线C的方程是
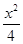 +y2=1.
+y2=1.(2)当直线l的斜率不存在时,显然不满足条件,所以设直线l的方程为y=kx-2,直线l与椭圆交于A(x1,y1),B(x2,y2)两点.
由
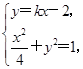 得(1+4k2)x2-16kx+12=0,
得(1+4k2)x2-16kx+12=0, 依题意Δ=(16k)2-48(1+4k2)>0,得k2>
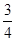 (*),
(*),此时x1+x2=
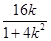 ,x1x2=
,x1x2=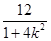 .
.因为
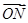 =
=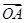 +
+ ,所以四边形OANB为平行四边形.
,所以四边形OANB为平行四边形.又四边形OANB是矩形,所以
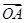 ·
· =0,
=0,即x1x2+y1y2=x1x2+k2x1x2-2k(x1+x2)+4=(1+k2)x1x2-2k(x1+x2)+4=0,
∴(1+k2)·
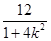 -2k·
-2k·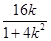 +4=0,
+4=0,解之得k2=4,∴k=±2.满足(*)式.
设N(x0,y0),由
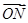 =
=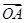 +
+ ,得
,得y0=y1+y2=k(x1+x2)-4=
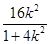 -4=-
-4=- ,
,从而点N在直线y=-
 上,满足题设,
上,满足题设,故直线l的方程为y=±2x-2.

练习册系列答案
相关题目
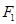 ,
,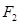 分别是椭圆
分别是椭圆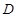 :
: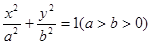 的左、右焦点,过
的左、右焦点,过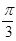 的直线交椭圆
的直线交椭圆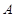 ,
,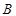 两点,
两点, 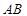 的距离为
的距离为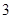 ,连结椭圆
,连结椭圆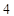 .
.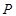 作直线
作直线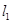 交椭圆
交椭圆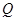 , 若点
, 若点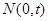 是线段
是线段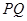 垂直平分线上的一点,且满足
垂直平分线上的一点,且满足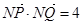 ,求实数
,求实数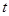 的值.
的值.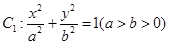 的离心率与双曲线
的离心率与双曲线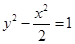 的离心率互为倒数,直线
的离心率互为倒数,直线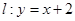 与以原点为圆心,以椭圆
与以原点为圆心,以椭圆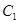 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切.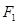 ,右焦点为
,右焦点为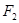 ,直线
,直线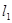 过点
过点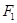 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线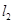 垂直
垂直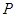 ,线段
,线段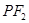 垂直平分线交
垂直平分线交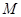 ,求点
,求点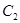 的方程;
的方程;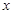 轴交于点
轴交于点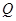 ,不同的两点
,不同的两点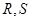 在
在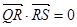 ,求
,求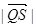 的取值范围.
的取值范围.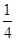 ,点P的轨迹为曲线C.
,点P的轨迹为曲线C.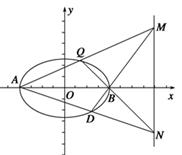
 +
+ =1
=1 +
+ =1
=1 =1
=1 =1
=1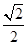 ,它的一个顶点为抛物线x2=4y的焦点.
,它的一个顶点为抛物线x2=4y的焦点.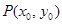 是椭圆
是椭圆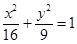 上一动点,
上一动点,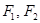 是椭圆的两个焦点,则
是椭圆的两个焦点,则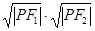 的最大值为 .
的最大值为 .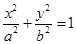
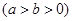 的两个焦点,若在C上存在一点P,使PF1⊥PF2,且∠PF1F2=30°,则C的离心率为_____________.
的两个焦点,若在C上存在一点P,使PF1⊥PF2,且∠PF1F2=30°,则C的离心率为_____________.