题目内容
【题目】
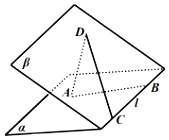
如图，在四面体
中，
、
分别是
、
的中点，
、
分别是
和
上的动点，且
与
相交于点
．下列判断中：
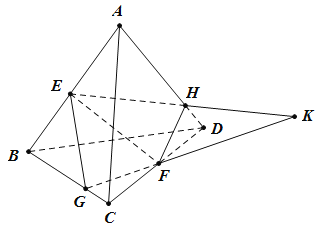
①直线
经过点；
②
；
③、、、四点共面，且该平面把四面体的体积分为相等的两部分．
所有正确的序号为
__________．
【答案】①③
【解析】
通过平面的基本性质与推论很容易证明三线共点，①正确；两个三角形的面积，一个为定值，另一个不是定值，②不正确；通过K点的特殊位置和运动，空间想象体积的变化，通过严谨的逻辑推理，得出结论③正确.
①项，因为
，所以
，且
平面
，
平面
同理可得， 
平面
；
又因为平面
平面
，所以
，
所以
，
，
三条直线相交于同一点.故①正确.
②项，
为定值，
为
上的动点，又因为与
为异面直线，
所以到的距离是变化的，所以
是变化的，故②不正确.
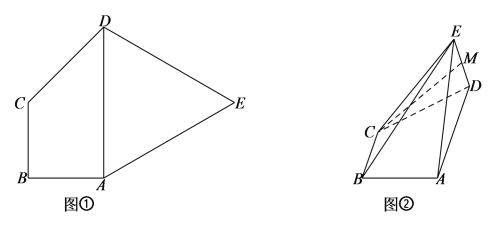
③ 项，当K与D重合时，H与D重合，G与C重合，如图（1）所示
此时平面EGFH即为平面ECD，
因为E为AB 中点，所以平面ECD把四面体分成体积相等的两部分.
图（1）
当K远离D时，平面EGFH使两部分体积发生了变化，
一部分在三棱锥A-ECD的基础上，
多出了一个三棱锥E-GCF的体积，如图2
少了一个三棱锥E-FDH的体积，如图3所示，
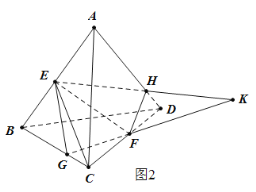
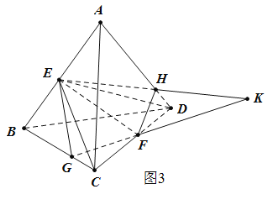
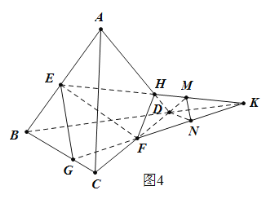
过点D做
，分别交EK，GK于点M，N，
连接MN，如图4所示
，
， 
，
，
，
所以无论
、
、
、如何变化，平面把四面体
的体积分为相等的两部分，③正确.
故答案为：①③
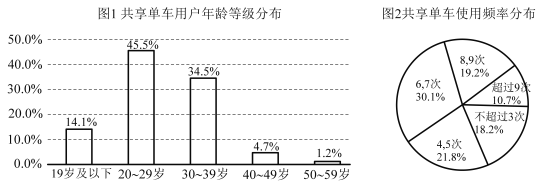
津桥教育计算小状元系列答案
【题目】共享单车进驻城市，绿色出行引领时尚．某市有统计数据显示，2020年该市共享单车用户年龄等级分布如图1所示，一周内市民使用单车的频率分布扇形图如图2所示．若将共享单车用户按照年龄分为“年轻人”（20岁－39岁）和“非年轻人”（19岁及以下或者40岁及以上）两类，将一周内使用的次数为6次或6次以上的称为“经常使用单车用户”，使用次数为5次或不足5次的称为“不常使用单车用户”．已知在“经常使用单车用户”中有
是“年轻人”．
（1）现对该市市民进行“经常使用共享单车与年龄关系”的调查，采用随机抽样的方法，抽取一个容量为200的样本，请你根据图表中的数据，补全下列
列联表，并根据列联表的独立性检验，判断是否有85%的把握认为经常使用共享单车与年龄有关？
年轻人 | 非年轻人 | 合计 | |
经常使用单车用户 | 120 | ||
不常使用单车用户 | 80 | ||
合计 | 160 | 40 | 200 |
使用共享单车情况与年龄列联表
（2）将（1）中频率视为概率，若从该市市民中随机任取3人，设其中经常使用共享单车的“非年轻人”人数为随机变量
，求的分布列与期望．
参考数据：独立性检验界值表
| 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
其中，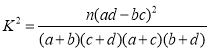
，
