题目内容
等差数列{an}的第3,7,10项成等比数列,则这个等比数列的公比q= .
【答案】分析:设公差d.首项为 a1,则由题意可得 (a1+6d)2=(a1+2d )(a1+9d ),解出d=0,即可得到公比q=1.
解答:解:设公差d.首项为 a1,则由题意可得 (a1+6d)2=(a1+2d )(a1+9d ),
∴a1=-18d,或d=0.
若 a1=-18d,则公比q=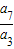 =
=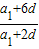 =
=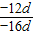 =
= .
.
若d=0,则此数列为常数数列,公比q=1.
综上可知,q= ,或q=1.
,或q=1.
故答案为 或 1.
或 1.
点评:本题考查等差数列的定义,等比数列的定义,求出公差d=0是解题的关键,体现了分类讨论的数学思想.
解答:解:设公差d.首项为 a1,则由题意可得 (a1+6d)2=(a1+2d )(a1+9d ),
∴a1=-18d,或d=0.
若 a1=-18d,则公比q=
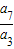 =
=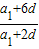 =
=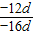 =
= .
.若d=0,则此数列为常数数列,公比q=1.
综上可知,q=
 ,或q=1.
,或q=1.故答案为
 或 1.
或 1.点评:本题考查等差数列的定义,等比数列的定义,求出公差d=0是解题的关键,体现了分类讨论的数学思想.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目