题目内容
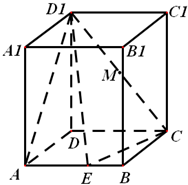 在长方体ABCD-A1B1C1D1中,AD=1,AA1=AB=2,点E是AB中点,点M为D1C的中点.
在长方体ABCD-A1B1C1D1中,AD=1,AA1=AB=2,点E是AB中点,点M为D1C的中点.(I)证明:直线ME∥平面ADD1A1;
(II)求二面角A-D1E-C的大小.
分析:(Ⅰ)当E为AB的中点时,ME∥平面ADD1A1.取DD1的中点N,连接MN、AN、ME,证明 ME∥AN,即可证明ME∥平面AD1.
(Ⅱ)当E为AB的中点时,结合二面角A-D1E-C的大小为二面角A-D1E-D与二面角D-D1E-C大小的和,只需求二面角A-D1E-D的大小即可;过A点作AF⊥DE交DE于F,过F作FH⊥D1E于H,连接AH,则∠AHF即为二面角A-D1E-D的平面角,通过AH•D1E=AE•AD1然后求出sin∠AHF,即可求出二面角A-D1E-C的大小.
(Ⅱ)当E为AB的中点时,结合二面角A-D1E-C的大小为二面角A-D1E-D与二面角D-D1E-C大小的和,只需求二面角A-D1E-D的大小即可;过A点作AF⊥DE交DE于F,过F作FH⊥D1E于H,连接AH,则∠AHF即为二面角A-D1E-D的平面角,通过AH•D1E=AE•AD1然后求出sin∠AHF,即可求出二面角A-D1E-C的大小.
解答: 证明:(Ⅰ)当E为AB的中点时,ME∥平面ADD1A1.
证明:(Ⅰ)当E为AB的中点时,ME∥平面ADD1A1.
证明:取DD1的中点N,连接MN、AN、ME,
MN∥
CD,AE∥
CD,
∴四边形MNAE为平行四边形,可知 ME∥AN
∵AN在平面AD1内
∴ME∥平面AD1.
(Ⅱ)当E为AB的中点时,DE=
,CE=
,又CD=2,
可知∠DEC=90°,所以DE⊥CE,平面CED1⊥平面DD1E,
所以二面角D-D1E-C的大小为
;
又二面角A-D1E-C的大小为二面角A-D1E-D与二面角D-D1E-C大小的和,
只需求二面角A-D1E-D的大小即可;
过A点作AF⊥DE交DE于F,则AF⊥平面DD1E,AF=
,
过F作FH⊥D1E于H,连接AH,
则∠AHF即为二面角A-D1E-D的平面角,
在Rt△AED1中,又AH•D1E=AE•AD1,
∴AH=
=
=
=
,
∴sin∠AHF=
=
=
,
所以二面角A-D1E-C的大小为
+arcsin
.
 证明:(Ⅰ)当E为AB的中点时,ME∥平面ADD1A1.
证明:(Ⅰ)当E为AB的中点时,ME∥平面ADD1A1.证明:取DD1的中点N,连接MN、AN、ME,
MN∥
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形MNAE为平行四边形,可知 ME∥AN
∵AN在平面AD1内
∴ME∥平面AD1.
(Ⅱ)当E为AB的中点时,DE=
| 2 |
| 2 |
可知∠DEC=90°,所以DE⊥CE,平面CED1⊥平面DD1E,
所以二面角D-D1E-C的大小为
| π |
| 2 |
又二面角A-D1E-C的大小为二面角A-D1E-D与二面角D-D1E-C大小的和,
只需求二面角A-D1E-D的大小即可;
过A点作AF⊥DE交DE于F,则AF⊥平面DD1E,AF=
| ||
| 2 |
过F作FH⊥D1E于H,连接AH,
则∠AHF即为二面角A-D1E-D的平面角,
在Rt△AED1中,又AH•D1E=AE•AD1,
∴AH=
| AE•AD1 |
| ED1 |
1×
| ||||
|
| ||
|
| ||
| 6 |
∴sin∠AHF=
| AF |
| AH |
| ||||
|
| ||
| 5 |
所以二面角A-D1E-C的大小为
| π |
| 2 |
| ||
| 5 |
点评:本题考查直线与平面平行,二面角的求法,考查转化思想,空间想象能力,计算能力.

练习册系列答案
相关题目
 在长方体ABCD-A'B'C'D'中,AB=
在长方体ABCD-A'B'C'D'中,AB= 如图,在长方体ABCD-A′B′C′D′中,用截面截下一个棱锥C-A′DD′,求棱锥C-A′DD′的体积与剩余部分的体积之比.
如图,在长方体ABCD-A′B′C′D′中,用截面截下一个棱锥C-A′DD′,求棱锥C-A′DD′的体积与剩余部分的体积之比. (2013•上海) 如图,在长方体ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离.
(2013•上海) 如图,在长方体ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离. (2009•青浦区二模)(理)在长方体ABCD-A'B'C'D'中,AB=2,AD=1,AA'=1.
(2009•青浦区二模)(理)在长方体ABCD-A'B'C'D'中,AB=2,AD=1,AA'=1. 已知在长方体ABCD-A′B′C′D′中,点E为棱CC′上任意一点,AB=BC=2,CC′=1.
已知在长方体ABCD-A′B′C′D′中,点E为棱CC′上任意一点,AB=BC=2,CC′=1.